Question

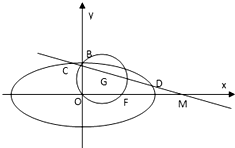如图，已知圆G：x²+y²-2x-

2

y=0经过椭圆

x2

a2

+

y2

b2

=1(a＞b＞0)的右焦点F及上顶点B．过点M（m，0）作倾斜角为

5

6

π的直线l交椭圆于C、D两点．
（1）求椭圆的方程；
（2）若点Q（1，0）恰在以线段CD为直径的圆的内部，求实数m范围．

Answer 1

分析：（1）利用已知即可得到点F，B的坐标，即可得到c，b，再利用a²=b²+c²即可；
（2）把直线的方程与椭圆的方程联立即可得到根与系数的关系，又点Q（1，0）在以线段CD为直径的圆内，即可得到

QC

•

QD

＜0．代入即可得到m的取值范围．

解答：解：（1）∵圆G：x2+y2-2x-

2

y=0经过椭圆的右焦点F及上顶点B．
∴F（2，0），B（0，

2

），∴c=2，b=

2

，
∴a²=b²+c²=6．
∴椭圆的方程为

x2

6

+

y2

2

=1．
（2）由题意l的方程为：y=-

3

3

(x-m)．
设C（x₁，y₁），D（x₂，y₂）．
联立

y=- 3 3 (x-m) x2 6 + y2 2 =1

，消去y整理得2x²-2mx+m²-6=0．
由△＞0得到4m²-4×2（m²-6）＞0，解得-2

3

＜m＜2

3

．
∴x₁+x₂=m，x1x2=

m2-6

2

．
又点Q（1，0）在以线段CD为直径的圆内，∴

QC

•

QD

＜0．
∴（x₁，y₁）•（x₂-1，y₂）＜0，
∴x1x2-(x1+x2)+1+(-

3

3

)2(x1-m)(x2-m)＜0．
∴

4

3

x1x2-(1+

1

3

m)(x1+x2)+

1

3

m2+1＜0．
∴2m²-3m-9＜0，
解得-

3

2

＜m＜3．
综上所述，m的取值范围是(-

3

2

，3)．

点评：熟练掌握椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立得到根与系数的关系、点在圆的内部的等价条件、一元二次不等式的解法等是解题的关键．