题目内容
18.已知数列{an}对任意的p,q∈N*满足:ap+q=2ap+2aq(p≠q),且a1=1,a2=4,那么an=-2+3•2n-1.分析 当n≥3时,利用an=2an-1+2整理可知数列{an+2}(n≥2)是以6为首项、以2为公比的等比数列,进而计算可得结论.
解答 解:依题意,当n≥3时,an=2an-1+2,
∴an+2=2(an-1+2),
又∵a2+2=4+2=6,
∴数列{an+2}(n≥2)是以6为首项、以2为公比的等比数列,
∴an+2=6•2n-2=3•2n-1,
∴an=-2+3•2n-1(n≥2),
又∵a1=1满足上式,
∴an=-2+3•2n-1,
故答案为:-2+3•2n-1.
点评 本题考查数列的通项,对表达式的灵活变形是解决本题的关键,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
9.关于直线a,b,c以及平面α,β,给出下列命题:
①若a∥α,b∥α,则a∥b
②若a∥α,b⊥α,则a⊥b
③若a?α,b?α,且c⊥a,c⊥b,则c⊥α
④若a⊥α,a∥β,则α⊥β.
其中错误的命题是( )
①若a∥α,b∥α,则a∥b
②若a∥α,b⊥α,则a⊥b
③若a?α,b?α,且c⊥a,c⊥b,则c⊥α
④若a⊥α,a∥β,则α⊥β.
其中错误的命题是( )
| A. | ①② | B. | ②④ | C. | ①③ | D. | ②③ |
6.如果一个水平放置的图形的斜二测直观图是一个边长为a的正方形,那么原平面四边形的面积等于( )
| A. | $\frac{{\sqrt{2}}}{4}a$2 | B. | $\frac{{\sqrt{2}}}{2}a$2 | C. | $2\sqrt{2}a$2 | D. | $\frac{{2\sqrt{2}}}{3}a$2 |
10.若$A_{2n}^3=9A_n^3$,则n等于( )
| A. | 12 | B. | 13 | C. | 14 | D. | 15 |
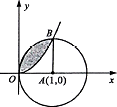 如图所示,阴影部分是由曲线y=x2(x>0)与圆(x-1)2+y2=1构成的区域,在圆中任取一点M,则M点落在阴影部分区域的概率为$\frac{1}{4}$-$\frac{1}{3π}$.
如图所示,阴影部分是由曲线y=x2(x>0)与圆(x-1)2+y2=1构成的区域,在圆中任取一点M,则M点落在阴影部分区域的概率为$\frac{1}{4}$-$\frac{1}{3π}$.