题目内容
8.若直角坐标平面内的两个不同点P、Q满足条件:①P、Q都在函数y=f(x)的图象上;
②P、Q关于原点对称,则称点对[P,Q]是函数y=f(x)的一对“友好点对”(注:点对[P,Q]与[Q,P]看作同一对“友好点对”).已知函数f(x)=$\left\{\begin{array}{l}{(\frac{1}{2})^{x},x>0}\\{-{x}^{2}-4x,x≤0}\end{array}\right.$,则此函数的“友好点对”有( ) 对.
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 根据题意可知只须作出函数y=$(\frac{1}{2})^{x}$(x>0)的图象关于原点对称的图象,确定它与函数y=-x2-4x(x≤0)交点个数即可.
解答 解:由题意得:
函数f(x)=$\left\{\begin{array}{l}{(\frac{1}{2})^{x},x>0}\\{-{x}^{2}-4x,x≤0}\end{array}\right.$,“友好点对”的对数,
等于函数(x>0)的图象关于原点对称的图象,与函数y=-x2-4x(x≤0)交点个数
在同一坐标系中做出函数y=$(\frac{1}{2})^{x}$(x>0)的图象关于原点对称的图象,与函数y=-x2-4x(x≤0)的图象如下图所示: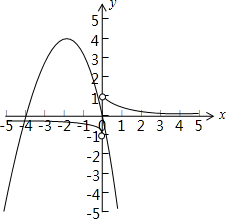
由图象可知,两个图象只有一个交点.
故选:B.
点评 本题考查的知识点是函数的图象,分段函数,新定义,其中将“友好点对”的对数转化为对应图象交点个数是解答的关键.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
16.对甲、乙两名自行车赛手在相同条件下进行了6次测试,测得他们的最大速度(m/s)的数据如下表.
(1)画出茎叶图.
(2)分别求出甲、乙两名自行车赛手最大速度(m/s)数据的平均数、中位数、极差,并判断选谁参加比赛更合适.
| 甲 | 27 | 38 | 30 | 37 | 35 | 31 |
| 乙 | 33 | 29 | 38 | 34 | 28 | 36 |
(2)分别求出甲、乙两名自行车赛手最大速度(m/s)数据的平均数、中位数、极差,并判断选谁参加比赛更合适.