题目内容
已知椭圆的焦点在y轴上,若椭圆 +
+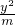 =1的离心率为
=1的离心率为 ,则m=
,则m=
- A.

- B.

- C.
 或
或
- D.
 或
或
B
分析:依题意椭圆的方程为: +
+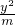 =1,可知a,进而根据离心率求得c,进而根据b2=a2-c2求得m.
=1,可知a,进而根据离心率求得c,进而根据b2=a2-c2求得m.
解答:由椭圆的方程为: +
+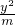 =1,且焦点在y轴上,
=1,且焦点在y轴上,
知,a= ,
,
?e= =
= =
= ,?c=
,?c= ,
,
由b2=a2-c2,得2=m- ,
,
则m=
故选B.
点评:本题主要考查了椭圆的标准方程、待定系数法等.解题的关键是熟练掌握椭圆标准方程中a,b和c之间的关系.
分析:依题意椭圆的方程为:
 +
+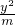 =1,可知a,进而根据离心率求得c,进而根据b2=a2-c2求得m.
=1,可知a,进而根据离心率求得c,进而根据b2=a2-c2求得m.解答:由椭圆的方程为:
 +
+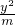 =1,且焦点在y轴上,
=1,且焦点在y轴上,知,a=
 ,
,?e=
 =
= =
= ,?c=
,?c= ,
,由b2=a2-c2,得2=m-
 ,
,则m=

故选B.
点评:本题主要考查了椭圆的标准方程、待定系数法等.解题的关键是熟练掌握椭圆标准方程中a,b和c之间的关系.

练习册系列答案
相关题目
 的焦点在y轴上,
的焦点在y轴上, 的取值范围是( )
的取值范围是( ) B.
B.  C.
C.
 D.
D.
