题目内容
函数f(x)=πx+log2x的零点所在区间为( )
A、(0,
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
考点:利用导数研究函数的单调性,函数零点的判定定理
专题:函数的性质及应用
分析:根据正比例函数和对数函数的单调性,结合函数单调性的性质“增+增=增”可判断函数f(x)=πx+log2x在定义域(0,+∞)上为增函数,进而再由零点判定定理得到答案.
解答:
解:∵y=πx和y=log2x在(0,+∞)上为增函数,
∴函数f(x)=πx+log2x在定义域(0,+∞)上为增函数,
又∵f(
)═
-2<0,f(
)=
-1>0,
故函数f(x)=πx+log2x的零点所在区间为(
,
),
故选:C
∴函数f(x)=πx+log2x在定义域(0,+∞)上为增函数,
又∵f(
| 1 |
| 4 |
| π |
| 4 |
| 1 |
| 2 |
| π |
| 2 |
故函数f(x)=πx+log2x的零点所在区间为(
| 1 |
| 4 |
| 1 |
| 2 |
故选:C
点评:本题考查的知识点是零点判定定理,其中分析出f(x)=πx+log2x在定义域(0,+∞)上为增函数,是解答的关键.

练习册系列答案
相关题目
已知向量
、
,|
|=2,
=(3,4),
与
夹角等于60°,则
•
等于( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、5 | ||||
B、
| ||||
C、5
| ||||
D、5
|
为了对某课题进行研究,用分层抽样方法从三所科研单位A、B、C的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人):则( )
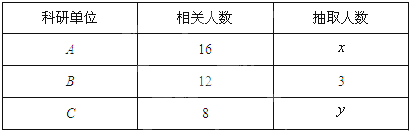

| A、x=6,y=4 |
| B、x=4,y=3 |
| C、x=7,y=4 |
| D、x=4,y=2 |
下列各式正确的是( )
A、
| |||
B、
| |||
C、
| |||
| D、a0=1 |
已知函数f(x)是偶函数,其图象与x轴有四个不同的交点,则函数f(x-1)的所有零点之和为( )
| A、0 | B、8 | C、4 | D、无法确定 |
 如图所示,a,b,c,d是四处处于断开状态的开关,任意将其两个闭合,则电路被接通的概率为( )
如图所示,a,b,c,d是四处处于断开状态的开关,任意将其两个闭合,则电路被接通的概率为( )| A、1 | ||
B、
| ||
C、
| ||
| D、0 |
f(x)=3x+5,g(x)=log3(x3-5),则y=f(g(x))是( )
| A、奇函数 |
| B、偶函数 |
| C、既是奇函数又是偶函数 |
| D、既不是奇函数又不是偶函数 |
若某组合体的三视图如图所示,则该几何体的体积为( )


A、
| ||
B、
| ||
| C、10 | ||
| D、12 |