题目内容
已知椭圆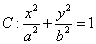
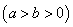 的右焦点
的右焦点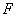
 ,长轴的左、右端点分别为
,长轴的左、右端点分别为 ,且
,且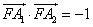 .
.
(Ⅰ)求椭圆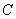 的方程;
的方程;
(Ⅱ)过焦点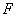 斜率为
斜率为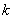
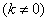 的直线
的直线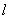 交椭圆
交椭圆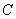 于
于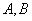 两点,弦
两点,弦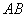 的垂直平分线与
的垂直平分线与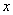 轴相交于点
轴相交于点 . 试问椭圆
. 试问椭圆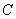 上是否存在点
上是否存在点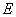 使得四边形
使得四边形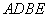 为菱形?若存在,试求点
为菱形?若存在,试求点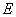 到
到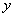 轴的距离;若不存在,请说明理由.
轴的距离;若不存在,请说明理由.
解:(Ⅰ)依题设 ,
, ,则
,则 ,
, .
.
由 ,解得
,解得 ,所以
,所以 .
.
所以椭圆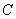 的方程为
的方程为 .
.
(Ⅱ)依题直线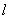 的方程为
的方程为 .
.
由 得
得 .
.
设 ,
, ,弦
,弦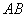 的中点为
的中点为 ,
,
则 ,
, ,
, ,
, ,
,
所以 .
.
直线 的方程为
的方程为 ,
,
令 ,得
,得 ,则
,则 .
.
若四边形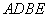 为菱形,则
为菱形,则 ,
, .
.
所以 .
.
若点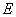 在椭圆
在椭圆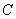 上,则
上,则 .
.
整理得 ,解得
,解得 .所以椭圆
.所以椭圆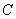 上存在点
上存在点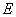 使得四边形
使得四边形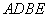 为菱形.
为菱形.
此时点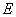 到
到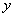 的距离为
的距离为 .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案
相关题目
 满足
满足 ,则下列不等式中一定成立的是
,则下列不等式中一定成立的是 B.
B.  C.
C.  D.
D. 
 义A*B={(x, y)| x∈A∩B, y∈A∪B},则A*B中元素个数是( )
义A*B={(x, y)| x∈A∩B, y∈A∪B},则A*B中元素个数是( ) B.
B. C.
C. D.
D.


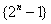 的前
的前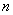 项
项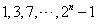 组成集合
组成集合 ,从集合
,从集合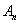 中任取
中任取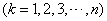 个数,其所有可能的
个数,其所有可能的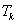 (若只取一个数,规定乘积为此数本身),记
(若只取一个数,规定乘积为此数本身),记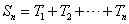 .例如当
.例如当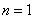 时,
时,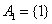 ,
,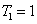 ,
,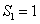 ;当
;当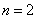 时,
时,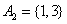 ,
,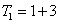 ,
,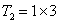 ,
, .则当
.则当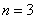 时,
时,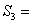 ;试写出
;试写出 .
. 分享到
分享到



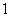

 的非空子集
的非空子集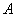 具有性质
具有性质 :当
:当 时,必有
时,必有 .则具有性质
.则具有性质



 为不等式组
为不等式组 表示的平面区域上一点,则
表示的平面区域上一点,则 取值范围为
取值范围为 (B)
(B) (C)
(C) (D)
(D)