题目内容

设f(x)=ax2+bx,且-1≤f(-1)≤2,2≤f(1)≤4,求f(-2)的取值范围.

解：由已知条件可转化为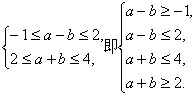

又f(-2)=4a-2b,这就是目标函数.

在关于a、b的直角坐标系中,作出可行域如下图,目标函数f(-2)=4a-2b分别在A、B两处取得最值.

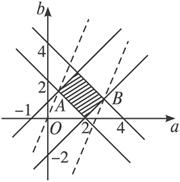
A点由方程组确定,解之，得

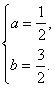
B点由方程组确定,解之把两组解分别代入f(-2)中得f(-2)的两个最值为-1和10,

∴-1≤f(-2)≤10.


练习册系列答案
相关题目
设f(x)=
ax2+bx
．
（1）当a=-1，b=4时，求函数f（ex）（e是自然对数的底数．）的定义域和值域；
（2）求满足下列条件的实数a的值：至少有一个正实数b，使函数f（x）的定义域和值域相同．
设f(x)=
ax2+bx
，求满足下列条件的实数a的值：至少有一个正实数b，使函数f（x）的定义域和值域相同．
设f(x)=ax2+c,且-3≤f(1)≤1,-2≤f(2)≤3，求f(3)的最大值与最小值.

设f(x)=ax2+bx满足-1≤f(-1)≤2,2≤f(1)≤4,求f(-2)的取值范围?.

设f(x)=ax2+bx,1≤f(-1)≤2,2≤f(1)≤4,求f(-2)的取值范围.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网