题目内容

19．已知斜三棱柱ABC-A1B1C1的体积为V，在斜三棱柱内任取一点P，则三棱锥P-ABC的体积大于$\frac{V}{5}$的概率为（　　）
A．$\frac{1}{5}$B．$\frac{2}{5}$C．$\frac{3}{5}$D．$\frac{4}{5}$

分析 设出P点到底面距离为h1，由题意得到满足三棱锥P-ABC的体积大于$\frac{V}{5}$的h1与原斜三棱柱高的关系得答案．

解答 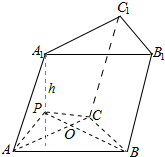解：如图，
设斜三棱柱ABC-A1B1C1的底面积为S，高为h，
P点到底面距离为h1，
则Sh=V，①
由$\frac{1}{3}S{h}_{1}=\frac{V}{5}$，得$S{h}_{1}=\frac{3V}{5}$，②
②÷①得：$\frac{{h}_{1}}{h}=\frac{3}{5}$，
∴三棱锥P-ABC的体积大于$\frac{V}{5}$的概率为$\frac{h-\frac{3}{5}h}{h}=\frac{2}{5}$．
故选：B．

点评 本题考查棱柱、棱锥的体积公式，考查了几何概型概率公式的应用，是中档题．

练习册系列答案
相关题目
4．有10名三好学生名额，分配给高二级6个班（可以分到一个班），有多少种分配方案？
10．已知函数$f（x）=sin（2x-\frac{π}{6}）$．
（I）求函数f（x）的最小正周期；
（Ⅱ）求函数f（x）的单调递增区间；
（Ⅲ）当$x∈[{0，\frac{2π}{3}}]$时，求函数f（x）的最小值，并求出使y=f（x）取得最小值时相应的x值．
7．已知函数f（x）是定义在R上的奇函数，且当x＞0时，f（x）=$\frac{3}{x}$-1
（Ⅰ）求f（0），f（-2）的值
（Ⅱ）用函数单调性的定义证明函数f（x）在（0，+∞）上是减函数．
14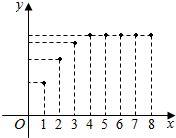．甲工厂八年来某种产品年产量与时间（单位：年）的函数关系如图所示．现有下列四种说法：
①前三年该产品产量增长速度越来越快；
②前三年该产品产量增长速度越来越慢；
③第三年后该产品停止生产；
④第三年后该产品年产量保持不变．
其中说法正确的是（　　）
A．①③B．①④C．②③D．②④
4．sin2016°的值为（　　）
A．正数B．负数C．零D．不存在
11．已知定义在R上的函数f（x），对任意的x，y∈R都有f（x+y）=f（x）+f（y），且当x＞0时，f（x）＞0．
（Ⅰ）求f（0）的值，判断f（x）的奇偶性并说明理由；
（Ⅱ）求证：f（x）在（-∞，+∞）上是增函数；
（Ⅲ）若不等式f（k•2x）+f（2x-4x-2）＜0对任意x∈R恒成立，求实数k的取值范围．
8．若将函数f（x）=x6表示为f（x）=a0+a1（1+x）+a2（1+x）2+…a6（1+x）6，其中a0，a1，a2，…，a6为实数，则a3等于 （　　）
A．20B．15C．-15D．-20
9．已知α，β，γ为不同的平面，l，m为不同的直线．若α∩β=l，m?α，l∥γ，m⊥γ．则（　　）
A．m∥βB．m⊥βC．l∥mD．l⊥m

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网