题目内容
9.已知函数f(x)=ln(1+x),x∈[0,+∞),f'(x)是f(x)的导函数.设g(x)=f(x)-axf'(x)(a为常数),求函数g(x)在[0,+∞)上的最小值.分析 求出函数g(x)的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的最小值.
解答 解:由题意$g(x)=ln({x+1})-\frac{ax}{1+x}$,
$g'(x)=\frac{1}{x+1}-\frac{{a({1+x})-ax}}{{{{({1+x})}^2}}}=\frac{x+1-a}{{{{({1+x})}^2}}}$…(2分)
令g'(x)>0,即x+1-a>0,得x>a-1,
当a-1≤0,即a≤1时,g(x)在[0,+∞)上单调递增,
gmin(x)=g(0)=ln(1+0)-0=0…(5分)
当a-1>0即a>1时,g(x)在[a-1,+∞)上单调递增,在[0,a-1]上单调递减,
所以g(x)min=h(a-1)=lna-a+1…(8分)
综上:$g{(x)_{min}}=\left\{{\begin{array}{l}{0,a≤1}\\{lna-a+1,a>1}\end{array}}\right.$…(10分)
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,是一道中档题.

练习册系列答案
相关题目
12.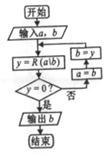 我国古代数学名著《九章算术》中的更相减损术的算法思路与右图类似.记R(a\b)为a除以b所得的余数(a,b∈N*),执行程序框图,若输入a,b分别为266,63,则输出的b的值为( )
我国古代数学名著《九章算术》中的更相减损术的算法思路与右图类似.记R(a\b)为a除以b所得的余数(a,b∈N*),执行程序框图,若输入a,b分别为266,63,则输出的b的值为( )
 我国古代数学名著《九章算术》中的更相减损术的算法思路与右图类似.记R(a\b)为a除以b所得的余数(a,b∈N*),执行程序框图,若输入a,b分别为266,63,则输出的b的值为( )
我国古代数学名著《九章算术》中的更相减损术的算法思路与右图类似.记R(a\b)为a除以b所得的余数(a,b∈N*),执行程序框图,若输入a,b分别为266,63,则输出的b的值为( )| A. | 1 | B. | 3 | C. | 7 | D. | 21 |
1.若关于x的不等式x2+2x-k>0的解集为R,则实数k的取值范围是( )
| A. | {k|k≤-1或k≥1} | B. | {k|-1<k<1} | C. | {k|k<-1} | D. | {k|k≤-1} |
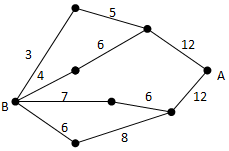 如图,小黑圆表示网络的结点,结点之间的连线表示它们有网线相连.连线上标注的数字表示该段网线单位时间内可以通过的最大信息量.现从结点A向结点B传递信息,信息可以分开沿不同的路线同时传递.则单位时间内传递的最大信息量为( )
如图,小黑圆表示网络的结点,结点之间的连线表示它们有网线相连.连线上标注的数字表示该段网线单位时间内可以通过的最大信息量.现从结点A向结点B传递信息,信息可以分开沿不同的路线同时传递.则单位时间内传递的最大信息量为( )