题目内容
13.若y=f(x)图象有两条对称轴x=a,x=b,(a≠b),则y=f(x)必是周期函数,且一周期为2|a-b|.分析 若y=f(x)图象有两条对称轴x=a,x=b,(a≠b),则y=f(x)必是周期函数,且一周期为2|a-b|,根据函数的对称性和周期性,可证得结论.
解答 解:若y=f(x)图象有两条对称轴x=a,x=b,(a≠b),
则y=f(x)必是周期函数,且一周期为2|a-b|,
理由如下:
由已知可得:f(x)=f(2a-x),且f(x)=f(2b-x),
不妨令a>b,
则f[x+(2a-2b)]=f(2a-x-2a+2b)=f(2b-x)=f(x),
即此时y=f(x)的周期为2a-2b;
同理可得:a<b时,y=f(x)的周期为2b-2a;
综上可得:y=f(x)的周期为2|a-b|.
故答案为:2|a-b|
点评 本题考查的知识点是抽象函数的周期性和对称性,难度中档.

练习册系列答案
相关题目
1.已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,双曲线 x2-y2=1的渐近线与椭圆C有四个交点,以这四个交点为顶点的四边形的面积为8,则椭圆C的方程为( )
| A. | $\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{2}$=1 | B. | $\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{6}$=1 | C. | $\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{3}$=1 | D. | $\frac{{x}^{2}}{20}$+$\frac{{y}^{2}}{5}$=1 |
1.已知定义在R上的函数f(x)满足:f(x+1)=$\sqrt{f(x){-f}^{2}(x)}+\frac{1}{2}$,数列{an}满足an=f2(n)-f(n),n∈N*,若其前n项和为-$\frac{35}{16}$,则n的值为( )
| A. | 16 | B. | 17 | C. | 18 | D. | 19 |
5.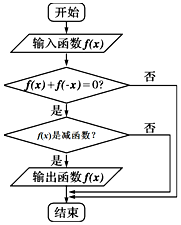 执行如图所示的程序框图,若输入如下四个函数:①f(x)=sinx,②f(x)=cosx,③f(x)=$\frac{1}{x}$,④f(x)=lg$\frac{1-x}{1+x}$,则输出的函数是( )
执行如图所示的程序框图,若输入如下四个函数:①f(x)=sinx,②f(x)=cosx,③f(x)=$\frac{1}{x}$,④f(x)=lg$\frac{1-x}{1+x}$,则输出的函数是( )
 执行如图所示的程序框图,若输入如下四个函数:①f(x)=sinx,②f(x)=cosx,③f(x)=$\frac{1}{x}$,④f(x)=lg$\frac{1-x}{1+x}$,则输出的函数是( )
执行如图所示的程序框图,若输入如下四个函数:①f(x)=sinx,②f(x)=cosx,③f(x)=$\frac{1}{x}$,④f(x)=lg$\frac{1-x}{1+x}$,则输出的函数是( )| A. | f(x)=sinx | B. | f(x)=cosx | C. | f(x)=$\frac{1}{x}$ | D. | f(x)=lg$\frac{1-x}{1+x}$ |
2.已知双曲线$\frac{x^2}{3}-\frac{y^2}{2}=1$的左,右焦点分别为F1,F2,O为坐标原点,圆O是以F1F2为直径的圆,直线$l:\sqrt{2}x+\sqrt{3}y+t=0$与圆O有公共点.则实数t的取值范围是( )
| A. | $[{-2\sqrt{2},2\sqrt{2}}]$ | B. | [-4,4] | C. | [-5,5] | D. | $[{-5\sqrt{2},5\sqrt{2}}]$ |
