题目内容
14.设复数z满足关系z•i=-1+$\frac{3}{4}$i,那么z=$\frac{3}{4}$+i.分析 根据复数的代数形式运算法则,求出z即可.
解答 解:复数z满足关系z•i=-1+$\frac{3}{4}$i,
∴z=$\frac{-1+\frac{3}{4}i}{i}$=$\frac{-i+{\frac{3}{4}i}^{2}}{{i}^{2}}$=$\frac{3}{4}$+i.
故答案为:$\frac{3}{4}$+i.
点评 本题考查了复数代数形式的运算问题,是基础题.

练习册系列答案
相关题目
4.已知集合S={1,2},设S的真子集有m个,则m=( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
5.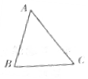 为了竖一块广告牌,要制造三角形支架,如图,要求∠ACB=60°,BC的长度大于1米,且AC比AB长0.5米,为了稳固广告牌,要求AC越短越好,则AC最短为( )
为了竖一块广告牌,要制造三角形支架,如图,要求∠ACB=60°,BC的长度大于1米,且AC比AB长0.5米,为了稳固广告牌,要求AC越短越好,则AC最短为( )
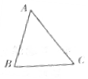 为了竖一块广告牌,要制造三角形支架,如图,要求∠ACB=60°,BC的长度大于1米,且AC比AB长0.5米,为了稳固广告牌,要求AC越短越好,则AC最短为( )
为了竖一块广告牌,要制造三角形支架,如图,要求∠ACB=60°,BC的长度大于1米,且AC比AB长0.5米,为了稳固广告牌,要求AC越短越好,则AC最短为( )| A. | (1+$\frac{\sqrt{3}}{2}$)米 | B. | 2米 | C. | (1+$\sqrt{3}$)米 | D. | (2+$\sqrt{3}$)米 |
1.已知定义在R上的函数f(x)满足:f(x+1)=$\sqrt{f(x){-f}^{2}(x)}+\frac{1}{2}$,数列{an}满足an=f2(n)-f(n),n∈N*,若其前n项和为-$\frac{35}{16}$,则n的值为( )
| A. | 16 | B. | 17 | C. | 18 | D. | 19 |
5.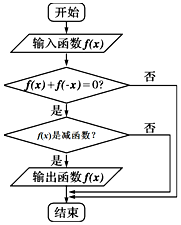 执行如图所示的程序框图,若输入如下四个函数:①f(x)=sinx,②f(x)=cosx,③f(x)=$\frac{1}{x}$,④f(x)=lg$\frac{1-x}{1+x}$,则输出的函数是( )
执行如图所示的程序框图,若输入如下四个函数:①f(x)=sinx,②f(x)=cosx,③f(x)=$\frac{1}{x}$,④f(x)=lg$\frac{1-x}{1+x}$,则输出的函数是( )
 执行如图所示的程序框图,若输入如下四个函数:①f(x)=sinx,②f(x)=cosx,③f(x)=$\frac{1}{x}$,④f(x)=lg$\frac{1-x}{1+x}$,则输出的函数是( )
执行如图所示的程序框图,若输入如下四个函数:①f(x)=sinx,②f(x)=cosx,③f(x)=$\frac{1}{x}$,④f(x)=lg$\frac{1-x}{1+x}$,则输出的函数是( )| A. | f(x)=sinx | B. | f(x)=cosx | C. | f(x)=$\frac{1}{x}$ | D. | f(x)=lg$\frac{1-x}{1+x}$ |
6.已知函数f(x)=$\left\{\begin{array}{l}{{e}^{x},x≥0}\\{ax,x<0}\end{array}\right.$若方程f(-x)=f(x)有五个不同的根,则实数a的取值范围为( )
| A. | (-∞,-e) | B. | (-∞,-1) | C. | (1,+∞) | D. | (e,+∞) |
