题目内容
(本题满分10分)选修4-4:坐标系与参数方程已知极坐标系的极点在直角坐标系的原点处,极轴与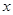 轴非负半轴重合.直线
轴非负半轴重合.直线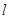 的参数方程为:
的参数方程为: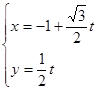 (
(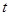 为参数),曲线
为参数),曲线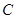 的极坐标方程为:
的极坐标方程为: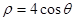 .
.
(1)写出曲线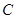 的直角坐标方程,并指明
的直角坐标方程,并指明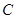 是什么曲线;
是什么曲线;
(2)设直线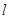 与曲线
与曲线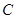 相交于
相交于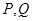 两点,求
两点,求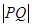 的值.2
的值.2
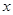 轴非负半轴重合.直线
轴非负半轴重合.直线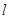 的参数方程为:
的参数方程为: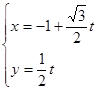 (
(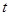 为参数),曲线
为参数),曲线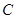 的极坐标方程为:
的极坐标方程为: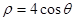 .
.(1)写出曲线
 的直角坐标方程,并指明
的直角坐标方程,并指明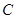 是什么曲线;
是什么曲线;(2)设直线
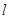 与曲线
与曲线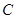 相交于
相交于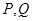 两点,求
两点,求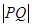 的值.2
的值.2(1) ,它是以
,它是以 为圆心,半径为
为圆心,半径为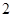 的圆.
的圆.
(2)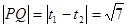 .
.
 ,它是以
,它是以 为圆心,半径为
为圆心,半径为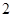 的圆.
的圆. (2)
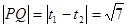 .
.本题主要考查把参数方程化为普通方程的方法,把极坐标方程化为直角坐标方程的方法,参数的几何意义,属于基础题.
(Ⅰ)由ρ=4cosθ可得ρ2=4ρcosθ,故曲线C的直角坐标方程为(x-2)2+y2=4,它是以(2,0)为圆心,半径为2的圆.
(Ⅱ)把参数方程代入x2+y2=4x整理得t2-3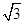 t+5=0,利用根与系数的关系求得t1+t2="3"
t+5=0,利用根与系数的关系求得t1+t2="3" 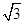 ,t1t2=5,根据 |PQ|=|t1-t2|求得结果
,t1t2=5,根据 |PQ|=|t1-t2|求得结果
解:(1)
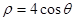 ,
,
 ,
,
由 ,
, ,得
,得
所以曲线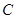 的直角坐标方程为
的直角坐标方程为 ,----2分
,----2分
它是以 为圆心,半径为
为圆心,半径为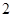 的圆.---4分
的圆.---4分
(2)把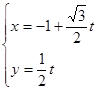 代入
代入 ,整理得
,整理得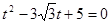 ,---6分
,---6分
设其两根分别为 则
则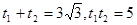 ,---8分
,---8分
所以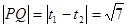 .----10分
.----10分
(Ⅰ)由ρ=4cosθ可得ρ2=4ρcosθ,故曲线C的直角坐标方程为(x-2)2+y2=4,它是以(2,0)为圆心,半径为2的圆.
(Ⅱ)把参数方程代入x2+y2=4x整理得t2-3
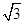 t+5=0,利用根与系数的关系求得t1+t2="3"
t+5=0,利用根与系数的关系求得t1+t2="3" 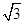 ,t1t2=5,根据 |PQ|=|t1-t2|求得结果
,t1t2=5,根据 |PQ|=|t1-t2|求得结果解:(1)

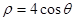 ,
,
 ,
,由
 ,
, ,得
,得
所以曲线
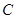 的直角坐标方程为
的直角坐标方程为 ,----2分
,----2分它是以
 为圆心,半径为
为圆心,半径为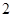 的圆.---4分
的圆.---4分(2)把
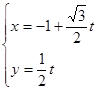 代入
代入 ,整理得
,整理得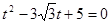 ,---6分
,---6分设其两根分别为
 则
则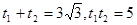 ,---8分
,---8分所以
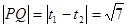 .----10分
.----10分
练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
 与
与 的两个圆的圆心距离为_________。
的两个圆的圆心距离为_________。 中,求曲线
中,求曲线 与
与 的交点
的交点 的极坐标.
的极坐标. 与点
与点 关于直线
关于直线 对称
对称 .
.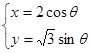
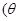 为参数)和定点
为参数)和定点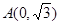 ,
,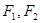 是此圆锥曲线的左、右焦点。
是此圆锥曲线的左、右焦点。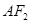 的极坐标方程;
的极坐标方程;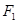 ,且与直线
,且与直线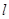 交此圆锥曲线于
交此圆锥曲线于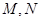 两点,求
两点,求 的值.
的值.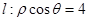 相交于点M,在OM上取一点P,使
相交于点M,在OM上取一点P,使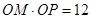 .
. (2)设R为
(2)设R为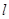 上任意一点,试求RP的最小值.
上任意一点,试求RP的最小值. ﹤
﹤ ),曲线
),曲线 与
与 的交点的极坐标为_______________
的交点的极坐标为_______________ 的直角坐标为
的直角坐标为 ,则点
,则点


