题目内容
【题目】设直线l的方程为（a+1）x+y+2﹣a=0（a∈R）
（1）若直线l在两坐标轴上的截距相等，则直线l的方程是；
（2）若直线l不经过第二象限，则实数a的取值范围是 ．
【答案】
（1）3x+y=0或x+y+2=0
（2）（﹣∞，﹣1]
【解析】解：（1.）令x=0，得y=a﹣2． 令y=0，得x= 
（a≠﹣1） ∵l在两坐标轴上的截距相等，∴a﹣2= ，解得a=2或a=0．
∴所求的直线l方程为3x+y=0或x+y+2=0．
（2.）直线l的方程可化为 y=﹣（a+1）x+a﹣2．
∵l不过第二象限，∴ 
，解得a≤﹣1．
∴a的取值范围为（﹣∞，﹣1]．
所以答案是：3x+y=0或x+y+2=0，（﹣∞，﹣1]
【考点精析】解答此题的关键在于理解截距式方程的相关知识，掌握直线的截距式方程：已知直线
与
轴的交点为A
，与
轴的交点为B
，其中
，以及对一般式方程的理解，了解直线的一般式方程：关于
的二元一次方程
（A，B不同时为0）．
练习册系列答案
相关题目
【题目】某种产品的质量以其质量指标值衡量，并依据质量指标值划分等极如下表：
质量指标值 |
|
|
|
等级 | 三等品 | 二等品 | 一等品 |
从某企业生产的这种产品中抽取200件，检测后得到如下的频率分布直方图：
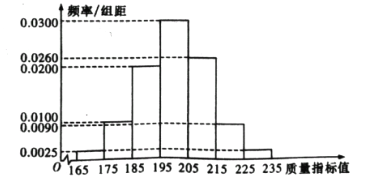
（1）根据以上抽样调查数据 ，能否认为该企业生产的这种产品符合“一、二等品至少要占全部产品90%”的规定？
（2）在样本中，按产品等极用分层抽样的方法抽取8件，再从这8件产品中随机抽取4件，求抽取的4件产品中，一、二、三等品都有的概率；
（3）该企业为提高产品质量，开展了“质量提升月”活动，活动后再抽样检测，产品质量指标值
近似满足
，则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少？
