Question

【题目】如图，在四边形ABCD中， R）， ， ，且△BCD是以BC为斜边的直角三角形．求：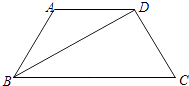
（1）λ的值；
（2） 的值．

Answer 1

【答案】
（1）解：因为 ，所以BC∥AD，且 ．

因为 ，所以 ．

又 ，所以 ．

作AH⊥BD于H，则H为BD的中点．

在Rt△AHB中，得 ，于是∠ABH=30°．

所以∠ADB=∠DBC=30°．

而∠BDC=90°，所以BD=BCcos30°，即 ，解得λ=2．

当∠BCD=900时，解得λ=1.5故λ=2或1.5

（2）解：由（1）知，∠ABC=60°，|

所以 与 的夹角为120°．

故

【解析】（1）由题意可知 且△ABD是三边分别为2，2， 的等腰三角形，利用已知条件可得∠ABD=30°，从而可得∠ABD=∠ADB=∠DBC=30°，解直角三角形可得λ（2）由（1）知，∠ABC=60°，| |=4，从而可得 的夹角1200 ， 代入向量的数量积公式，即可．