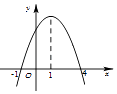题目内容
【题目】函数
图象上不同两点
， 
处切线的斜率分别是
， 
，规定
（
为线段
的长度）叫做曲线
在点
与
之间的“弯曲度”，给出以下命题：
①函数
图象上两点
与
的横坐标分别为1和2，则
；
②存在这样的函数，图象上任意两点之间的“弯曲度”为常数；
③设点
， 
是抛物线
上不同的两点，则
；
④设曲线
（
是自然对数的底数）上不同两点
， 
，且
，若
恒成立，则实数
的取值范围是
．
其中真命题的序号为__________．（将所有真命题的序号都填上）
【答案】②③
【解析】对于①，由
得
，
故
，
又
，故
。
∴
。故①错误。
对于②，常数函数y=1满足图象上任意两点之间的“弯曲度”为常数，故②正确；
对于③，设
， 
，又
，
∴
，
∴
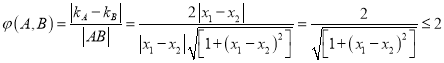，故③正确。
对于④，由
可得
， 
，
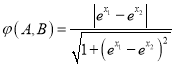由
恒成立可得
恒成立，
而当
时该式恒成立，故④错误。
综上可得②③正确。
答案：②③
练习册系列答案
相关题目
