Question

【题目】如图，在四棱锥中，底面是菱形， 平面， 是棱上的一个动点．

（Ⅰ）若为的中点，求证： 平面；

（Ⅱ）求证：平面平面；

（Ⅲ）若三棱锥的体积是四棱锥体积的，求的值．

Answer 1

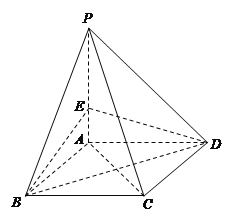
【答案】（Ⅰ）见解析；（Ⅱ）见解析；（Ⅲ） .

【解析】试题分析：(1)欲证平面，即证，借助中位线性质易证；（2）欲证平面平面，即证平面;(3) =,而， ，易得结果.

试题解析：

（Ⅰ）证明：如图，设交于,连接．

因为底面是菱形，

所以是的中点．

又因为为的中点，

所以．

因为平面, 平面，

所以平面．

（Ⅱ）证明：因为底面是菱形，

所以．

又因为平面， 平面，

所以．

因为，

所以平面．

因为平面，

所以平面平面．

（Ⅲ）设四棱锥的体积为．

因为平面，所以．

又因为底面是菱形，

所以，

所以．

根据题意， ，

所以．

又因为，

所以．