题目内容
(理)已知⊙ :
: 和定点
和定点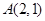 ,由⊙
,由⊙ 外一点
外一点 向⊙
向⊙ 引切线
引切线 ,切点为
,切点为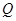 ,且满足
,且满足 .
.
(1)求实数 间满足的等量关系;
间满足的等量关系;
(2)求线段 长的最小值;
长的最小值;
(3)若以 为圆心所作的⊙
为圆心所作的⊙ 与⊙
与⊙ 有公共点,试求半径取最小值时的⊙
有公共点,试求半径取最小值时的⊙ 方程.
方程.
 :
: 和定点
和定点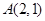 ,由⊙
,由⊙ 外一点
外一点 向⊙
向⊙ 引切线
引切线 ,切点为
,切点为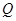 ,且满足
,且满足 .
.(1)求实数
 间满足的等量关系;
间满足的等量关系;(2)求线段
 长的最小值;
长的最小值;(3)若以
 为圆心所作的⊙
为圆心所作的⊙ 与⊙
与⊙ 有公共点,试求半径取最小值时的⊙
有公共点,试求半径取最小值时的⊙ 方程.
方程.(1) ;(2)
;(2)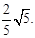 ;(3)
;(3)
 ;(2)
;(2)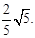 ;(3)
;(3)
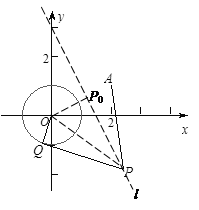
试题分析:(1)连接OP,OQ,
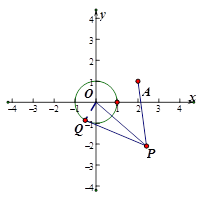
则
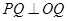 ,在
,在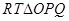 中,
中,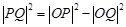 ,且
,且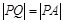 ,结合两点之间距离公式可得关于
,结合两点之间距离公式可得关于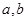 的等式;(2)在
的等式;(2)在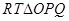 中,
中,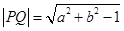 ,是含有
,是含有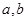 的二元函数,结合(1)可得关于
的二元函数,结合(1)可得关于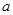 的一元函数,求其最小值即可;(3)方法一:因为⊙
的一元函数,求其最小值即可;(3)方法一:因为⊙ 与⊙
与⊙ 有公共点,则得圆心距和其半径的关系
有公共点,则得圆心距和其半径的关系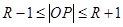 即
即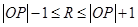 ,要求半径
,要求半径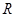 的最小值,只需
的最小值,只需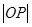 最小,将
最小,将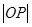 用两点之间距离公式表示出来,求其最小值并求取的最小值时
用两点之间距离公式表示出来,求其最小值并求取的最小值时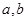 ,得⊙
,得⊙ 的圆心,进而求出圆的标准方程;方法二:由(1)知⊙
的圆心,进而求出圆的标准方程;方法二:由(1)知⊙ 的圆心的轨迹方程为
的圆心的轨迹方程为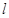 :
: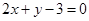 ,过点
,过点 作垂直于
作垂直于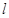 的垂线,垂足为
的垂线,垂足为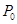 ,当两圆外切且以
,当两圆外切且以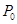 为圆心时,半径最小,此时
为圆心时,半径最小,此时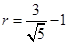 ,两条直线求交点确定圆心,从而求出圆的 标准方程.
,两条直线求交点确定圆心,从而求出圆的 标准方程.试题解析:(1)连
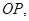
 为切点,
为切点,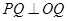 ,由勾股定理有
,由勾股定理有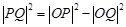 ,又由已知
,又由已知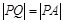 ,故
,故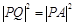 .即:
.即: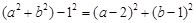 ,化简得实数a、b间满足的等量关系为:
,化简得实数a、b间满足的等量关系为: ;(2)由
;(2)由 ,得
,得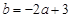 ,
,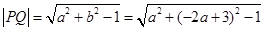
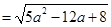 =
=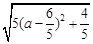 ,故当
,故当 时,
时, 即线段PQ长的最小值为
即线段PQ长的最小值为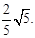 ;
;(3)方法一:设圆P的半径为
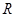 ,
, 圆P与圆O有公共点,圆O的半径为1,
圆P与圆O有公共点,圆O的半径为1,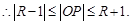 即
即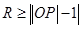 且
且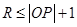 ,而
,而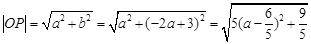 ,故当
,故当 时,
时,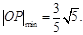 此时,
此时, 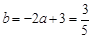 ,
,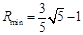 ,得半径取最小值时圆P的方程为
,得半径取最小值时圆P的方程为 .
.方法二:圆
 与圆
与圆 有公共点,圆
有公共点,圆 半径最小时为与圆外
半径最小时为与圆外 切(取小者)的情形,而这些半径的最小值为圆心
切(取小者)的情形,而这些半径的最小值为圆心 到直线
到直线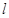 的距离减去1,圆心为
的距离减去1,圆心为 过原点与
过原点与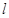 垂直的直线
垂直的直线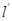 与
与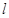 的交点
的交点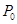 ,
,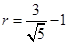 ,又
,又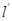 :x-2y = 0,解方程组
:x-2y = 0,解方程组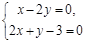 ,得
,得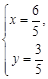 .即
.即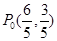 ,∴所求圆方程为
,∴所求圆方程为 .
.

练习册系列答案
相关题目
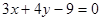 和
和 的距离是_______.
的距离是_______.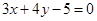 与圆
与圆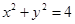 相交于
相交于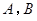 两点,那么弦
两点,那么弦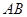 的长等于 ( )
的长等于 ( ) 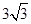
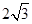
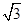
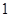
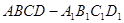 ,下列说法正确的有: ____________.
,下列说法正确的有: ____________.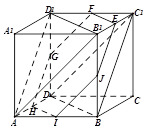
 点在线段
点在线段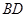 上运动,棱锥
上运动,棱锥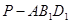 体积不变;
体积不变;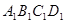 平行;
平行;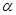 截此正方体,如果截面是三角形,则必为锐角三角形;
截此正方体,如果截面是三角形,则必为锐角三角形;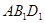 与平面
与平面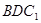 间平行移动时此六边形周长先增大,后减小。
间平行移动时此六边形周长先增大,后减小。 ,棱长为1,黑白二蚁都从点
,棱长为1,黑白二蚁都从点 出发,沿棱向前爬行,每走一条棱称为“走完一段”.白蚁爬行的路线是
出发,沿棱向前爬行,每走一条棱称为“走完一段”.白蚁爬行的路线是 黑蚁爬行的路线是
黑蚁爬行的路线是 它们都遵循如下规则:所爬行的第
它们都遵循如下规则:所爬行的第 段所在直线与第
段所在直线与第 段所在直线必须是异面直线(其中
段所在直线必须是异面直线(其中 ).设黑白二蚁走完第2014段后,各停止在正方体的某个顶点处,这时黑白蚁的距离是 ( )
).设黑白二蚁走完第2014段后,各停止在正方体的某个顶点处,这时黑白蚁的距离是 ( )


 的棱长为2,则
的棱长为2,则 与平面
与平面 间的距离为__________。
间的距离为__________。 的距离
的距离 .
.