题目内容
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() :
: ![]() 和圆
和圆![]() :
: ![]() .
.
(1)若直线![]() 过点
过点![]() ,且被圆
,且被圆![]() 截得的弦长为
截得的弦长为![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)设![]() 为平面直角坐标系上的点,满足:存在过点
为平面直角坐标系上的点,满足:存在过点![]() 的无穷多对相互垂直的直线
的无穷多对相互垂直的直线![]() 和
和![]() ,它们分别与圆
,它们分别与圆![]() 和
和![]() 相交,且直线
相交,且直线![]() 被圆
被圆![]() 截得的弦长与直线
截得的弦长与直线![]() 被圆
被圆![]() 截得的弦长相等,试求所有满足条件的点
截得的弦长相等,试求所有满足条件的点![]() 的坐标.
的坐标.
【答案】(1)直线![]() 的方程为
的方程为![]() 或
或![]() ;(2)点
;(2)点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
【解析】试题分析:(1)因为直线![]() 过点
过点![]() ,故可以设出直线
,故可以设出直线![]() 的点斜式方程,又由直线被圆
的点斜式方程,又由直线被圆![]() 截得的弦长为
截得的弦长为![]() 根据半弦长、半径、弦心距满足勾股定理,我们可以求出弦心距, 即圆心到直线的距离,得到一个关于直线斜率
根据半弦长、半径、弦心距满足勾股定理,我们可以求出弦心距, 即圆心到直线的距离,得到一个关于直线斜率![]() 的方程, 解方程求出
的方程, 解方程求出![]() 值, 代入即得直线
值, 代入即得直线![]() 的方程;(2)与(1)相同,我们可以设出过
的方程;(2)与(1)相同,我们可以设出过![]() 点的直线
点的直线![]() 与
与![]() 的点斜式方程,由于两直线斜率为
的点斜式方程,由于两直线斜率为![]() ,且直线
,且直线![]() 被圆
被圆![]() 截得的弦长与直线
截得的弦长与直线![]() 被圆
被圆![]() 截得的弦长相等,故我们可以得到一个关于直线斜率
截得的弦长相等,故我们可以得到一个关于直线斜率![]() 的方程,解方程求出
的方程,解方程求出![]() 值,代入即得直线
值,代入即得直线![]() 与
与![]() 的方程.
的方程.
试题解析:(1)由于直线![]() 与圆
与圆![]() 不相交;
不相交;
∴直线![]() 的斜率存在,设
的斜率存在,设![]() 方程为:
方程为: ![]() ,
,
圆![]() 的圆心到直线
的圆心到直线![]() 的距离为
的距离为![]() ,∵
,∵![]() 被
被![]() 截得的弦长为
截得的弦长为![]() ,
,
∴![]() 从而
从而![]() 即
即![]() ,
,
∴直线![]() 的方程为:
的方程为: ![]()
(2)设点![]() 满足条件,
满足条件,
由题意分析可得直线![]() 的斜率均存在且不为0,
的斜率均存在且不为0,
不妨设直线![]() 的方程为
的方程为![]() ,
,
则直线![]() 的方程为:
的方程为: ![]() ,
,
∵![]() 和
和![]() 的半径相等,及直线
的半径相等,及直线![]() 被圆
被圆![]() 截得的弦长与直线
截得的弦长与直线![]() 被圆
被圆![]() 截得的弦长相等,
截得的弦长相等,
∴![]() 的圆心到直线
的圆心到直线![]() 的距离和圆
的距离和圆![]() 的圆心到直线
的圆心到直线![]() 的距离相等,
的距离相等,
即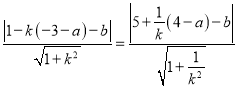 ,
,
整理得![]() ,
,
∴![]() ,
,
即![]() 或
或![]() ,
,
因![]() 的取值有无穷多个,所以
的取值有无穷多个,所以![]() 或
或![]() ,
,
解得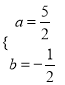 或
或 这样的点只可能是点
这样的点只可能是点![]() 或点
或点![]() .
.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目