题目内容
下列命题中,正确的是
(1)曲线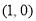 在点
在点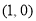 处的切线方程是
处的切线方程是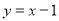 ;
;
(2)函数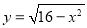 的值域是
的值域是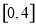 ;
;
(3)已知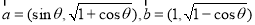 ,其中
,其中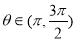 ,则
,则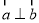 ;
;
(4)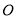 是
是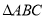 所在平面上一定点,动点P满足:
所在平面上一定点,动点P满足: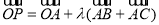 ,
,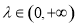 ,则
,则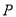 点的轨迹一定通过
点的轨迹一定通过 的重心;
的重心;
(1)(2)(3)(4)
【解析】
试题分析:(1)中 ,曲线在点
,曲线在点 处的切线的斜率
处的切线的斜率 ,切线方程为
,切线方程为 ,(1)正确;
,(1)正确;
(2)中由于 ,则
,则 ,(2)正确;(3)由于
,(2)正确;(3)由于
= +
+
 ,
, ,则
,则 ,
, 是非零向量,则
是非零向量,则 ,(3)对,(4)由于
,(3)对,(4)由于 ,以为邻边做平行四边形的对角线
,以为邻边做平行四边形的对角线 必通过
必通过 的中点,,必有
的中点,,必有
 ,
, 的轨迹为
的轨迹为 的
的 边的中线,所以
边的中线,所以 必通过
必通过 的重心.(4)正确
的重心.(4)正确
考点:1.导数的几何意义;2.函数的值域;3.平面向量;
考点分析: 考点1:导数及其应用 考点2:函数的定义域 考点3:函数的值域 【知识点的认识】函数值的集合{f(x)|x∈A}叫做函数的值域.A是函数的定义域.【解题方法点拨】(1)求函数的值域
此类问题主要利用求函数值域的常用方法:配方法、分离变量法、单调性法、图象法、换元法、不等式法等.
无论用什么方法求函数的值域,都必须考虑函数的定义域.
(2)函数的综合性题目
此类问题主要考查函数值域、单调性、奇偶性、反函数等一些基本知识相结合的题目.
此类问题要求考生具备较高的数学思维能力和综合分析能力以及较强的运算能力.
在今后的命题趋势中综合性题型仍会成为热点和重点,并可以逐渐加强.
(3)运用函数的值域解决实际问题
此类问题关键是把实际问题转化为函数问题,从而利用所学知识去解决.此类题要求考生具有较强的分析能力和数学建模能力.
【命题方向】函数的值域及其求法是近几年高考考查的重点内容之一,有时在函数与导数的压轴题中出现,是常考题型. 试题属性
- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
(本小题满分12分)
为了研究某种细菌在特定环境下,随时间变化繁殖情况,得如下实验数据:
天数t(天) | 3 | 4 | 5 | 6 | 7 |
繁殖个数y(千个) | 2.5 | 3 | 4 | 4.5 | 6 |
(Ⅰ)求y关于t的线性回归方程;
(Ⅱ)利用(Ⅰ)中的回归方程,预测 时,细菌繁殖个数.
时,细菌繁殖个数.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
 ,
, .
.
 ,集合
,集合 ,则
,则 ( )
( )



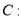
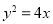 上一点
上一点 到
到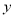 轴的距离为
轴的距离为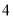 ,则点
,则点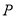 到抛物线
到抛物线 的焦点的距离是( )
的焦点的距离是( )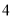 B.
B.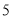 C.
C.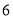 D.
D.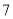
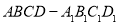 中,底面
中,底面 是正方形,
是正方形,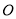 是
是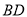 中点,点
中点,点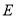 是棱
是棱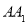 上任意一点.
上任意一点.
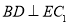 ;
;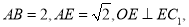 求
求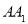 的长
的长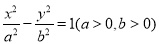 的一个焦点到一条渐近线的距离为
的一个焦点到一条渐近线的距离为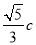 (
(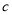 为双曲线的半焦距长),则该双曲线的离心率为( )
为双曲线的半焦距长),则该双曲线的离心率为( )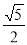 B.
B.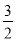 C.
C.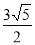 D.
D.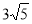
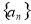 中,
中, 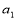 ,
,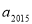 为方程
为方程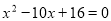 的两根,则
的两根,则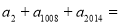 ( )
( )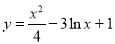 的一条切线的斜率为
的一条切线的斜率为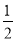 ,则切点的横坐标为( )
,则切点的横坐标为( )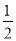
 化为十进制数,结果为 .
化为十进制数,结果为 .