题目内容
如图,已知⊙O中,直径AB垂直于弦CD,垂足为M,P是CD延长线上一点,PE切⊙O于点E,连接BE交CD于点F,证明:
(1)∠BFM=∠PEF;
(2)PF2=PD·PC.

(1)连接OE,
 ∵PE切⊙O于点E,∴OE⊥PE.
∵PE切⊙O于点E,∴OE⊥PE.
∴∠PEF+∠FEO=90°.
又∵AB⊥CD,
∴∠B+∠BFM=90°.[来源:Z*xx*k.Com][来源:学科网]
又∵∠B=∠FEO,
∴∠BFM=∠PEF.
(2)∵∠EFP=∠BFM,
∴∠EFP=∠PEF.
∴PE=PF.
又∵PE2=PD·PC,
∴PF2=PD·PC.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
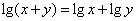 ,那么正确的选项是
,那么正确的选项是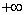 )上的减函数,且x+y
)上的减函数,且x+y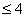
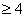
 和等比数列
和等比数列 首项都是1,公差与公比都是2,则
首项都是1,公差与公比都是2,则 ( )
( ) 中,
中, ,
, ,
, 分别为角
分别为角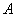 ,
, ,
, 的对边,
的对边, ,且
,且 .
. ,求
,求 B.
B. C.
C. D.
D.
 的值为
的值为 ,则输出的
,则输出的
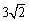 ,点M,N分别在PA,BD上,且
,点M,N分别在PA,BD上,且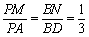 .
. (2)求MN与平面PAD所成角的正弦值.
(2)求MN与平面PAD所成角的正弦值.