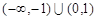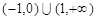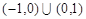题目内容
已知函数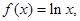 ,
, 直线与函数
直线与函数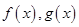 的图象都相切,且与
的图象都相切,且与 图象的切点为(1,f(x)),则
图象的切点为(1,f(x)),则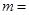 ( )
( )
A. | B. | C. | D. |
D
解析试题分析: 中
中
 ,所以切线为
,所以切线为 ,与
,与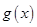 相切,联立方程组,方程组由唯一解,由二次方程
相切,联立方程组,方程组由唯一解,由二次方程 得
得
考点:曲线与直线切线及导数的几何意义
点评:几何意义:函数在某一点处的导数值等于该点处的切线斜率,直线与曲线相切常从切点入手,切点坐标同时满足两方程

练习册系列答案
相关题目
曲线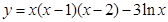 在点
在点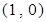 处的切线方程为( )
处的切线方程为( )
A.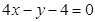 | B.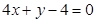 |
C. | D.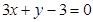 |
对于R上的可导的任意函数 ,若满足
,若满足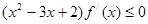 ,则函数
,则函数 在区间
在区间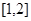 上必有( )
上必有( )
A. | B.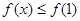 |
C.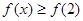 | D.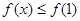 或 或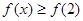 |
设函数 及其导函数
及其导函数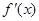 都是定义在R上的函数,则“
都是定义在R上的函数,则“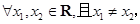
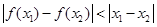 ”是“
”是“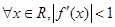 ”的
”的
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
“函数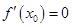 ”是“可导函数
”是“可导函数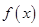 在点
在点 处取到极值”的 条件。 ( )
处取到极值”的 条件。 ( )
| A.充分不必要 | B.必要不充分 | C.充要 | D.既不充分也不必要 |
曲线 在
在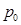 处的切线平行于直线
处的切线平行于直线 ,则
,则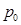 点的坐标为( )
点的坐标为( )
A.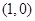 | B.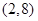 |
C.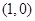 和 和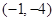 | D.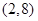 和 和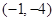 |
若曲线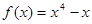 在点P处的切线平行于直线
在点P处的切线平行于直线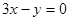 ,则点P的坐标为 ( )
,则点P的坐标为 ( )
| A.(1,0) | B.(1,5) | C.(1,-3) | D.(-1,2) |
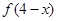
 ,且当
,且当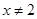
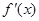 满足
满足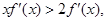
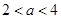
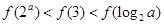
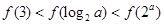
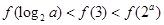
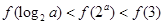
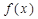 是定义在R上的奇函数,且
是定义在R上的奇函数,且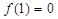 ,当
,当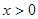 时,有
时,有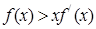 恒成立,则不等式
恒成立,则不等式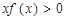 的解集为( )
的解集为( )