题目内容
已知函数f（x）=|x+1|+2|x-1|．
（Ⅰ）解不等式f（x）＜4；
（Ⅱ）若不等式f（x）≥|a+1|对任意的x∈R恒成立，求实数a的取值范围．
（Ⅰ）解不等式f（x）＜4；
（Ⅱ）若不等式f（x）≥|a+1|对任意的x∈R恒成立，求实数a的取值范围．
考点：带绝对值的函数
专题：选作题,不等式
分析：（Ⅰ）利用绝对值的几何意义，写出分段函数，即可解不等式f（x）＜4；
（Ⅱ）不等式f（x）≥|a+1|对任意的x∈R恒成立等价于|a+1|≤2，即可求实数a的取值范围．
（Ⅱ）不等式f（x）≥|a+1|对任意的x∈R恒成立等价于|a+1|≤2，即可求实数a的取值范围．
解答：
解：（I）f(x)=
．…（1分）
当x≤-1时，由-3x+1＜4得x＞-1，此时无解；
当-1＜x≤1时，由-x+3＜4得x＞-1，∴-1＜x≤1；
当x＞1时，由3x-1＜4得x＜
，∴1＜x＜
．…（4分）
综上，所求不等式的解集为{x|-1＜x＜
}．…（5分）
（II）由（I）的函数解析式可以看出函数f（x）在（-∞，1）单调递减，在（1，+∞）单调递增，故f（x）在x=1处取得最小值，最小值为f（1）=2，…（7分）
不等式f（x）≥|a+1|对任意的x∈R恒成立等价于|a+1|≤2，
即-2≤a+1≤2，解得-3≤a≤1，故a的取值范围为{a|-3≤a≤1}．…（10分）
|
当x≤-1时，由-3x+1＜4得x＞-1，此时无解；
当-1＜x≤1时，由-x+3＜4得x＞-1，∴-1＜x≤1；
当x＞1时，由3x-1＜4得x＜
| 5 |
| 3 |
| 5 |
| 3 |
综上，所求不等式的解集为{x|-1＜x＜
| 5 |
| 3 |
（II）由（I）的函数解析式可以看出函数f（x）在（-∞，1）单调递减，在（1，+∞）单调递增，故f（x）在x=1处取得最小值，最小值为f（1）=2，…（7分）
不等式f（x）≥|a+1|对任意的x∈R恒成立等价于|a+1|≤2，
即-2≤a+1≤2，解得-3≤a≤1，故a的取值范围为{a|-3≤a≤1}．…（10分）
点评：本题主要考查函数的恒成立问题，绝对值不等式的解法，关键是去掉绝对值，化为与之等价的不等式组来解，体现了分类讨论、转化的数学思想，属于中档题．
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
计算∫
cosxdx=（ ）
0 |
| A、-1 | ||
| B、1 | ||
C、
| ||
| D、0 |
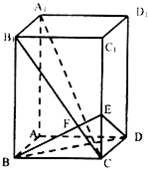已知长方体AC1中，棱AB=BC=1，棱BB1=2，连结B1C，过B点作B1C的垂线交CC1于E，交B1C于F．