题目内容
【题目】在圆![]() 上任取一点
上任取一点![]() ,过点
,过点![]() 作
作![]() 轴的垂线段,垂足为
轴的垂线段,垂足为![]() ,点
,点![]() 在线段
在线段![]() 上,且
上,且![]() ,当点
,当点![]() 在圆上运动时.
在圆上运动时.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
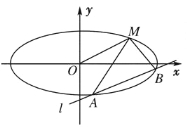
(2)设直线![]() 与上述轨迹
与上述轨迹![]() 相交于M、N两点,且MN的中点在直线
相交于M、N两点,且MN的中点在直线![]() 上,求实数k的取值范围.
上,求实数k的取值范围.
【答案】(1)点![]() 的轨迹C方程为
的轨迹C方程为![]() =
=![]() ;(2)k的取值范围是
;(2)k的取值范围是 .
.
【解析】试题分析:(1)设![]() ,由
,由![]() =
=![]() 得,
得, ![]() ,由
,由![]() ,得点
,得点![]() 的轨迹C方程为
的轨迹C方程为![]() ;(2)联立直线与椭圆方程,由根与系数的关系式,结合MN的中点在直线
;(2)联立直线与椭圆方程,由根与系数的关系式,结合MN的中点在直线![]() 上,可得
上,可得![]() =
=![]() ,结合
,结合![]() 求解,可得k的取值范围是
求解,可得k的取值范围是 .
.
解析:
(1)设![]() ,
,
由![]() 得,
得, ![]() =
= ![]() =
= ![]() ,
,
∵点![]() 在圆
在圆![]() 上,即
上,即![]() =
=![]() ,
,
∴![]() ,即
,即![]() =
=![]() ,
,
∴点![]() 的轨迹C方程为
的轨迹C方程为![]() =
=![]() .
.
(2)设![]() ,若直线l与x轴平行,
,若直线l与x轴平行,
则MN的中点在y轴上,与已知矛盾,所以![]() ,
,
把![]() 代入
代入![]() =
=![]() ,
,
得![]() =
=![]() ,
,
则![]() =
=![]() ,
,
由![]() ,得
,得![]() ,
,
由![]() ,得
,得![]() =
=![]() ,
,
所以![]() =
=![]() ,
,
解得![]() ,
,
所以k的取值范围是 .
.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目