题目内容
已知函数f (x) = 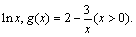
(1)试判断当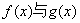 的大小关系;
的大小关系;
(2)试判断曲线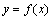 和
和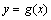 是否存在公切线,若存在,求出公切线方程,若不存在,说明理由;
是否存在公切线,若存在,求出公切线方程,若不存在,说明理由;
(3)试比较 (1 + 1×2) (1 + 2×3) ……(1 +2012×2013)与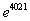 的大小,并写出判断过程.
的大小,并写出判断过程.
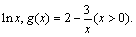
(1)试判断当
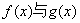 的大小关系;
的大小关系;(2)试判断曲线
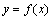 和
和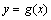 是否存在公切线,若存在,求出公切线方程,若不存在,说明理由;
是否存在公切线,若存在,求出公切线方程,若不存在,说明理由;(3)试比较 (1 + 1×2) (1 + 2×3) ……(1 +2012×2013)与
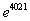 的大小,并写出判断过程.
的大小,并写出判断过程.(1) ;
;
(2)方程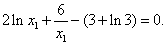 无解,故二者没有公切线。
无解,故二者没有公切线。
(3) (1 + 1×2) (1 + 2×3) ……(1 +2012×2013) 。
。
 ;
;(2)方程
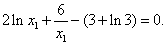 无解,故二者没有公切线。
无解,故二者没有公切线。(3) (1 + 1×2) (1 + 2×3) ……(1 +2012×2013)
 。
。试题分析:(1)设
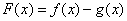 ,则
,则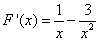 1分
1分由
 ,
,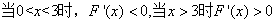
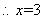 时, 2分
时, 2分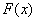 在区间
在区间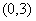 单调递减,在区间
单调递减,在区间 单调递增, 3分
单调递增, 3分所以
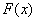 取得最小值为
取得最小值为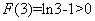 ,
,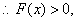 即
即 4分
4分(2)假设曲线
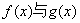 有公切线,切点分别为
有公切线,切点分别为 和
和 5分
5分因为
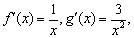 ,所以分别以
,所以分别以 和
和 为切线的切线方程为
为切线的切线方程为 6分
6分令
 即
即 8分
8分令
 所以由
所以由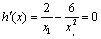 得
得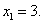 显然,当
显然,当 时,
时, ,当
,当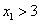 时,
时, ,所以
,所以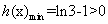 , 9分
, 9分所以方程
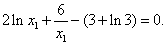 无解,故二者没有公切线。 10分
无解,故二者没有公切线。 10分(3)由(1)得
 对任意的x>0都成立,
对任意的x>0都成立, 11分
11分ln(1 + 1×2) + ln(1 + 2×3) + …+ln[1 + n (n + 1)]>

 =
= 令
令 =2012, 13分
=2012, 13分则ln(1 + 1×2) + ln(1 + 2×3) + …+ln(1 + 2012×2013) >2×2012-3=4021,
所以(1 + 1×2) (1 + 2×3) ……(1 +2012×2013)
 14分
14分点评:典型题,本题属于导数应用中的基本问题,通过研究函数的单调性,明确了极值情况。涉及比较大小问题,通过构造函数,转化成了研究函数的单调性及最值。涉及对数函数,要特别注意函数的定义域。

练习册系列答案
相关题目
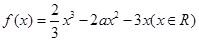 .
.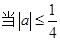 时,求证
时,求证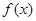 在
在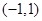 内是减函数;
内是减函数;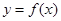 在
在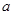 的取值范围.
的取值范围.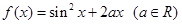 ,若对任意实数
,若对任意实数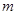 ,直线
,直线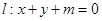
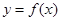 的切线,则
的切线,则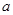 的取值范围是
的取值范围是 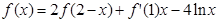 ,则
,则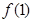 等于( )
等于( )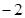
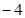
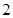
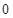

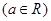 .
. 是曲线
是曲线 上任意一点, 则点
上任意一点, 则点 的距离的最小值是( )
的距离的最小值是( )

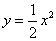 与直线
与直线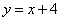 所围成的图形的面积是
所围成的图形的面积是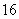
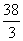
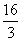
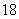
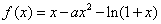 ,其中
,其中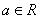 .
.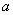 =1时,求
=1时,求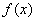 在(1,
在(1,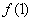 )的切线方程
)的切线方程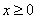 时,
时,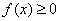 ,求实数
,求实数 ,则
,则 .
.