题目内容
点 是曲线
是曲线 上任意一点, 则点
上任意一点, 则点 到直线
到直线 的距离的最小值是( )
的距离的最小值是( )
 是曲线
是曲线 上任意一点, 则点
上任意一点, 则点 到直线
到直线 的距离的最小值是( )
的距离的最小值是( )| A.1 | B. | C.2 | D. |
B
试题分析:求出平行于直线y=x-2且与曲线y=x2-lnx相切的切点坐标,再利用点到直线的距离公式可得结论。解:设P(x,y),则y′=2x-
 (x>0),令2x-
(x>0),令2x- =1,则(x-1)(2x+1)=0,∵x>0,∴x=1,∴y=1,即平行于直线y=x+2且与曲线y=x2-lnx相切的切点坐标为(1,1),由点到直线的距离公式可得d=
=1,则(x-1)(2x+1)=0,∵x>0,∴x=1,∴y=1,即平行于直线y=x+2且与曲线y=x2-lnx相切的切点坐标为(1,1),由点到直线的距离公式可得d= ,故选B.
,故选B.点评:本题考查导数知识的运用,考查点到直线的距离公式,考查学生的计算能力,属于基础题.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
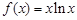 .
. 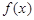 的最小值;
的最小值;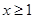 都有
都有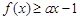 ,求实数
,求实数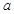 的取值范围.
的取值范围.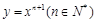 在点(1,1)处的切线与x轴的交点的横坐标为
在点(1,1)处的切线与x轴的交点的横坐标为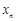 ,令
,令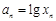 ,则
,则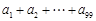 的值为 .
的值为 .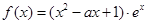 .
.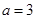 时,求曲线
时,求曲线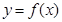 在点
在点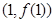 处的切线方程;
处的切线方程;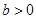 ,
,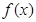 在区间
在区间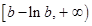 上是增函数,求实数
上是增函数,求实数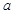 的取值范围.
的取值范围.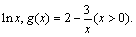
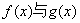 的大小关系;
的大小关系;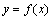 和
和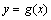 是否存在公切线,若存在,求出公切线方程,若不存在,说明理由;
是否存在公切线,若存在,求出公切线方程,若不存在,说明理由;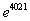 的大小,并写出判断过程.
的大小,并写出判断过程. .
. 在点
在点 处的切线方程;
处的切线方程; 为曲线
为曲线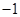 ≤a≤1,
≤a≤1,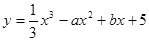 有极值的概率为( )
有极值的概率为( )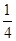
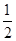
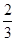
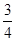
 ,则
,则 等于
等于 
