题目内容
已知A,B,C,D是同一球面上的四个点,其中△ABC是正三角形,AD⊥平面ABC,AD=2AB=6,则该球的表面积为( )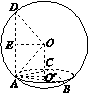
| A.16π | B.24π | C.32 π π | D.48π |
D
解析

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
已知圆锥的底面半径为 ,高为
,高为 ,在它的所有内接圆柱中,全面积的最大值为( )
,在它的所有内接圆柱中,全面积的最大值为( )
A. | B. | C. | D. |
已知四棱锥 的三视图如图,则四棱锥
的三视图如图,则四棱锥 的全面积为( )
的全面积为( )
A. | B. |
| C.5 | D.4 |
如图,在正三棱锥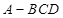 中,
中,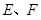 分别是
分别是 的中点,
的中点, ,且
,且 ,则正三棱锥
,则正三棱锥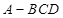 的体积是( )
的体积是( )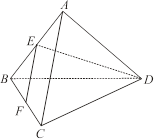
A. | B.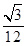 | C.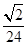 | D. |
某几何体的三视图如图所示,则该几何体的体积为( ).
| A.16+8π | B.8+8π | C.16+16π | D.8+16π |
体积为4 π的球的内接正方体的棱长为( ).
π的球的内接正方体的棱长为( ).
A.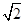 | B.2 | C. | D. |





