题目内容
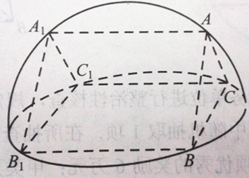
如图,在正三棱锥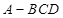 中,
中,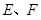 分别是
分别是 的中点,
的中点, ,且
,且 ,则正三棱锥
,则正三棱锥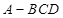 的体积是( )
的体积是( )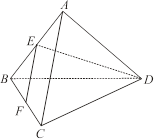
A. | B.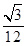 | C.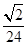 | D. |
C
解析试题分析:如图,取线段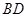 的中点
的中点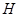 ,连接
,连接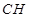 ,则依题意可知
,则依题意可知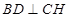 ,且顶点
,且顶点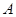 在底面
在底面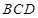 的射影
的射影 落在
落在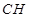 上,所以由
上,所以由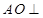 面
面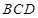 可得
可得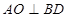 ,而
,而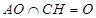 ,所以由线面垂直的判定定理可得
,所以由线面垂直的判定定理可得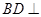 平面
平面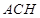 ,所以有
,所以有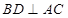 ,而
,而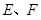 是边
是边 的中点,所以
的中点,所以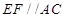 ,而
,而 ,所以
,所以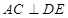 ,而
,而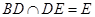 ,由线面垂直的判定定理又可以得到
,由线面垂直的判定定理又可以得到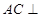 平面
平面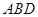 ,再结合三棱锥
,再结合三棱锥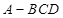 为正三棱锥且
为正三棱锥且 ,所以该正三棱锥的侧棱两两垂直且
,所以该正三棱锥的侧棱两两垂直且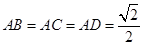 ,所以
,所以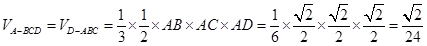 ,故选C.
,故选C.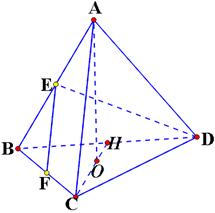
考点:1.空间中的垂直问题;2.三棱锥的体积问题.

练习册系列答案
相关题目
某几何体的三视图如图所示,则它的体积等于( )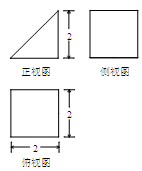
A.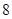 | B.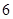 | C. | D.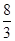 |
一个多面体的直观图、主视图、左视图、俯视图如下, 、
、 分别为
分别为 、
、 的中点.
的中点.
下列结论中正确的个数有( )
①直线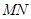 与
与 相交. ②
相交. ②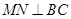 . ③
. ③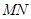 //平面
//平面 .
.
④三棱锥 的体积为
的体积为 .
.
| A.4个 | B.3个 | C.2个 | D.1个 |
圆柱的底面积为S,侧面展开图为正方形,那么这个圆柱的侧面积为( )
A. | B. | C. | D. |
右图是边长相等的两个正方形.给定下列三个命题:
①存在三棱柱,其正视图、侧视图如右图;
②存在四棱柱,其正视图、侧视图如右图;
③存在圆柱,其正视图、侧视图如右图.
其中真命题的个数是
| A.3 | B.2 | C.1 | D.0 |
已知一个几何体的三视图如图所示,则这个几何体的体积是( )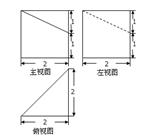
A.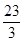 | B.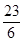 | C. | D.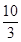 |
已知A,B,C,D是同一球面上的四个点,其中△ABC是正三角形,AD⊥平面ABC,AD=2AB=6,则该球的表面积为( )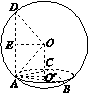
| A.16π | B.24π | C.32 π π | D.48π |
如图所示,则根据图中数据可知该几何体的体积为( ).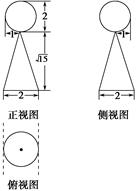
| A.8π | B.9π | C.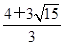 π π | D.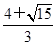 π π |
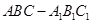 的六个顶点都在半径为1的半球面上,
的六个顶点都在半径为1的半球面上, ,侧面
,侧面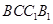 是半球底面圆的内接正方形,则侧面
是半球底面圆的内接正方形,则侧面 的面积为( )
的面积为( )