题目内容
已知圆锥的底面半径为 ,高为
,高为 ,在它的所有内接圆柱中,全面积的最大值为( )
,在它的所有内接圆柱中,全面积的最大值为( )
A. | B. | C. | D. |
B
解析试题分析:设内接圆柱的底面半径为 ,高为
,高为 ,全面积为
,全面积为 ,则有
,则有


 当
当 时,
时, 取最大值
取最大值 ,故选B.
,故选B.
考点:1.空间几何体的结构特征;2.圆柱的表面积;3.实际问题中的最值问题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
一个几何体的三视图如图所示,其中主视图和左视图是腰长为4的两个全等的等腰直角三角形,若该几何体的所有顶点在同一球面上,则该球的表面积是( )
| A.12π | B.24π |
| C.32π | D.48π |
如图是一个空间几何体的三视图,则该几何体的侧面积为( )
A. | B.4 | C.8 | D.12 |
一个与球心距离为1的平面截球体所得的圆面面积为π,则球的体积为( )
A. | B. | C. | D.8π |
网格纸中的小正方形边长为1,一个正三棱锥的侧视图如图所示,则这个正三棱锥的体积为( )
A. | B.3 | C. | D.  |
已知A,B,C,D是同一球面上的四个点,其中△ABC是正三角形,AD⊥平面ABC,AD=2AB=6,则该球的表面积为( )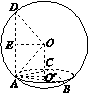
| A.16π | B.24π | C.32 π π | D.48π |
如图所示,则根据图中数据可知该几何体的体积为( ).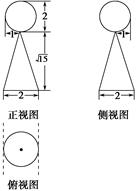
| A.8π | B.9π | C.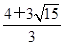 π π | D.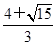 π π |
