题目内容
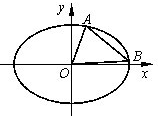
 如图A、B是椭圆
如图A、B是椭圆| x2 |
| a2 |
| y2 |
| b2 |
(1)求椭圆的离心率;
(2)若AB=3,求椭圆的方程.
分析:(1)椭圆的离心率,即求
,只需求a、c的值或a、c用同一个量表示.本题没有具体数值,因此只需把a、c用同一量表示,由PF1⊥OX,OP∥AB.易得b=c,a=
c.
(2)首先求出AB=3,得出所以c=
,a=
,即可求出方程
| c |
| a |
| 2 |
(2)首先求出AB=3,得出所以c=
| 3 |
| 6 |
解答:解:(1)PF1=
,OF1=c,OA=b,OB=a,
因为PF1⊥OX,OP∥AB,所以
=
,可得:b=c,
所以a=
c,故e=
;…(7分)
(2)AB=
c=3,所以c=
,故a=
,
所以椭圆的标准方程为:
+
=1.…(7分)
| b2 |
| a |
因为PF1⊥OX,OP∥AB,所以
| PF1 |
| OF1 |
| OA |
| OB |
所以a=
| 2 |
| ||
| 2 |
(2)AB=
| 3 |
| 3 |
| 6 |
所以椭圆的标准方程为:
| x2 |
| 6 |
| y2 |
| 3 |
点评:本题主要考查了椭圆的性质.要充分理解椭圆性质中的长轴、短轴、焦距、准线方程等概念及其关系.属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 A组:直角坐标系xoy中,已知中心在原点,离心率为
A组:直角坐标系xoy中,已知中心在原点,离心率为
 的椭圆E的一个焦点为圆C:x2+y2-4x+2=0的圆心.
的椭圆E的一个焦点为圆C:x2+y2-4x+2=0的圆心. 的直线l1,l2.当直线l1,l2都与圆C相切时,求P的坐标.
的直线l1,l2.当直线l1,l2都与圆C相切时,求P的坐标. 的左、右焦点分别为F1(-c,0),F2(c,0).已知点(1,e)和
的左、右焦点分别为F1(-c,0),F2(c,0).已知点(1,e)和 都在椭圆上,其中e为椭圆离心率.
都在椭圆上,其中e为椭圆离心率. ,求直线AF1的斜率.
,求直线AF1的斜率.
 的椭圆E的一个焦点为圆C:x2+y2-4x+2=0的圆心.
的椭圆E的一个焦点为圆C:x2+y2-4x+2=0的圆心. 的直线l1,l2.当直线l1,l2都与圆C相切时,求P的坐标.
的直线l1,l2.当直线l1,l2都与圆C相切时,求P的坐标. 的左、右焦点分别为F1(-c,0),F2(c,0).已知点(1,e)和
的左、右焦点分别为F1(-c,0),F2(c,0).已知点(1,e)和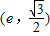 都在椭圆上,其中e为椭圆离心率.
都在椭圆上,其中e为椭圆离心率. ,求直线AF1的斜率.
,求直线AF1的斜率.