题目内容
如图,已知椭圆的中心在原点,左焦点为![]() ,右顶点为
,右顶点为![]() ,设点
,设点![]() .
.
⑴求该椭圆的标准方程;w.w.w.k.s.5.u.c.o.m ![]()
![]()
⑵过点A的直线l交椭圆于MN两点,点A为MN的中点,求直线l的方程;
 ⑶过原点
⑶过原点![]() 的直线交椭圆于点
的直线交椭圆于点![]() ,求
,求![]() 面积的最大值.
面积的最大值.
解析:(1)由已知得椭圆的半长轴a=2,半焦距c=![]() ,则半短轴b=1.
,则半短轴b=1.
又椭圆的焦点在x轴上, ∴椭圆的标准方程为![]() w.w.w.k.s.5.u.c.o.m
w.w.w.k.s.5.u.c.o.m ![]()
![]()
(2)设M(x1,y1),N(x2,y2)
由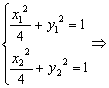
![]() ,
,
∵A为MN的中点, ∴![]()
∴![]()
![]() 即斜率
即斜率 ![]()
∴直线l的方程是:![]() 即x+2y-2=0.
即x+2y-2=0.
(3)当直线BC垂直于x轴时,BC=2,因此△ABC的面积S△ABC=1.
当直线BC不垂直于x轴时,设该直线方程为y=kx,代入![]() ,
,
解得B(![]() ,
,![]() ),C(-
),C(-![]() ,-
,-![]() ),
),
则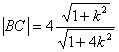 ,又点A到直线BC的距离d=
,又点A到直线BC的距离d=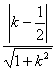 ,
,
∴△ABC的面积S△ABC=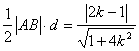
于是S△ABC=![]()
当k=0时,S=1;![]() 时,∵
时,∵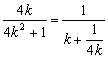
且![]() 则
则 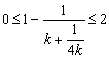 且
且![]()
∴S△ABC≤![]() ,其中,当k=-
,其中,当k=-![]() 时,等号成立.
时,等号成立.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
 如图,已知椭圆的中心在坐标原点,焦点F1,F2在x轴上,长轴A1A2的长为4,左准线l与x轴的交点为M,|MA1|:|A1F1|=2:1.
如图,已知椭圆的中心在坐标原点,焦点F1,F2在x轴上,长轴A1A2的长为4,左准线l与x轴的交点为M,|MA1|:|A1F1|=2:1. 如图,已知椭圆的中心在原点,焦点在x轴上,长轴长是短轴长的2倍且经过点M(2,1),平行于OM的直线l在y轴上的截距为m(m≠0),l交椭圆于A、B两个不同点.
如图,已知椭圆的中心在原点,焦点在x轴上,长轴长是短轴长的2倍且经过点M(2,1),平行于OM的直线l在y轴上的截距为m(m≠0),l交椭圆于A、B两个不同点. 如图,已知椭圆的中心在原点,焦点在x轴上,离心率为
如图,已知椭圆的中心在原点,焦点在x轴上,离心率为 如图,已知椭圆的中心在坐标原点,焦点在x轴上,它的一个顶点为A(0,
如图,已知椭圆的中心在坐标原点,焦点在x轴上,它的一个顶点为A(0, (2012•马鞍山二模)如图,已知椭圆的中心在原点,焦点在x轴上,长轴长是短轴长的2倍且经过点M(2,1),平行于OM的直线l在y轴上的截距为m(m≠0),直线l交椭圆于A、B两个不同点(A、B与M不重合).
(2012•马鞍山二模)如图,已知椭圆的中心在原点,焦点在x轴上,长轴长是短轴长的2倍且经过点M(2,1),平行于OM的直线l在y轴上的截距为m(m≠0),直线l交椭圆于A、B两个不同点(A、B与M不重合).