题目内容
15.函数f(x)的定义域为[-1,1],图象如图1所示;函数g(x)的定义域为[-1,2],图象如图2所示.A={x|f(g(x))=0},B={x|g(f(x))=0},则A∩B中元素的个数为( )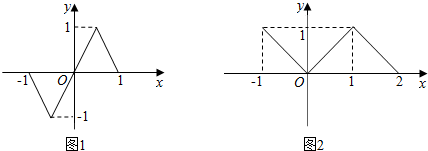
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 结合图象,分别求出集合A,B,再根据交集的定义求出A∩B,问题得以解决.
解答 解:由图象可知,
若f(g(x))=0,
则g(x)=0或g(x)=1,
由图2知,g(x)=0时,x=0,或x=2,
g(x)=1时,x=1或x=-1
故A={-1,0,1,2},
若g(f(x))=0,
由图1知,f(x)=0,或f(x)=2(舍去),
当f(x)=0时,x=-1或0或1,
故B={-1,0,1},
所以A∩B={-1,0,1},
则A∩B中元素的个数为3个.
故选:C.
点评 本题考查了方程的根与函数的图象的关系应用及数形结合的思想应用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.设函数f(x)=min{x2-1,x+1,-x+1},其中min{x,y,z}表示x,y,z中的最小者.若f(a+2)>f(a),则实数a的取值范围为( )
| A. | (-1,0) | B. | [-2,0] | C. | (-∞,-2)∪(-1,0) | D. | [-2,+∞) |
20.已知O为坐标原点,点A(-1,2),若点M(x,y)为平面区域$\left\{\begin{array}{l}{x+y≥2}\\{x≤1}\\{y≤2}\end{array}\right.$上的一个动点,则$\overrightarrow{OA}$•$\overrightarrow{OM}$的取值范围是( )
| A. | [-1,0] | B. | [0,1] | C. | [1,3] | D. | [1,4] |
7.函数$f(x)=\frac{1}{3}{x^3}-{x^2}-3x+5$的零点的个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
4.若抛物线y2=2px(p>0)的焦点为F,其准线经过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的左焦点,点M为这两条曲线的一个交点,且|MF|=p,则双曲线的离心率为( )
| A. | $\frac{{2+\sqrt{2}}}{2}$ | B. | $2+\sqrt{2}$ | C. | $1+\sqrt{2}$ | D. | $\frac{{1+\sqrt{2}}}{2}$ |