题目内容
已知函数f(x)=ax2+1(a>0),g(x)=x3+bx.
(1)若曲线y=f(x)与曲线y=g(x)在它们的交点(1,c)处具有公共切线,求a,b的值;
(2)当a=3,b=-9时,若函数f(x)+g(x)在区间[k,2]上的最大值为28,求k的取值范围.
解:(1)f′(x)=2ax,g′(x)=3x2+b.
因为曲线y=f(x)与曲线y=g(x)在它们的交点(1,c)处具有公共切线,所以f(1)=g(1),且f′(1)=g′(1),
即a+1=1+b,且2a=3+b,
解得a=3,b=3.
(2)记h(x)=f(x)+g(x),当a=3,b=-9时,
h(x)=x3+3x2-9x+1,
h′(x)=3x2+6x-9.
令h′(x)=0,得x1=-3,x2=1.
h(x)与h′(x)在(-∞,2]上的变化情况如下:
| x | (-∞,-3) | -3 | (-3,1) | 1 | (1,2) | 2 |
| h′(x) | + | 0 | - | 0 | + | |
| h(x) | 28 | -4 | 3 |

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
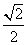 ,则该椭圆的方程为( )
,则该椭圆的方程为( )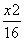 +
+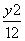 =1 B.
=1 B.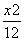 +
+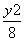 =1
=1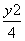 =1 D.
=1 D.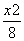 +
+ 的方程
的方程 在区间
在区间 上有实数解,则实数
上有实数解,则实数 的最大值为 。
的最大值为 。 +tan θ,则f′(0)=________.
+tan θ,则f′(0)=________. 的递增区间是 .
的递增区间是 . 中,已知
中,已知 ,则A=
,则A=  B.
B. C.
C. D.
D.
 、
、 ,过
,过 ,若
,若 为等腰直角三角形,则椭圆的离心率是 ( )
为等腰直角三角形,则椭圆的离心率是 ( ) (B)
(B) (C)
(C) (D)
(D)