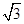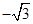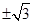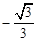题目内容
已知数列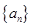 中,
中,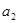 =
=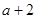 (
(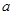 为常数);
为常数);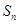 是
是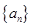 的前
的前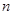 项和,且
项和,且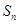 是
是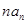 与
与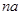 的等差中项。
的等差中项。
(1)求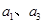 ;
;
(2)猜想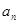 的表达式,并用数学归纳法加以证明;
的表达式,并用数学归纳法加以证明;
(3)求证以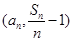 为坐标的点
为坐标的点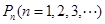 都落在同一直线上。
都落在同一直线上。
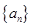 中,
中,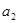 =
=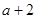 (
(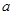 为常数);
为常数);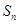 是
是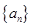 的前
的前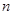 项和,且
项和,且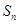 是
是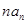 与
与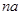 的等差中项。
的等差中项。(1)求
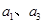 ;
;(2)猜想
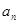 的表达式,并用数学归纳法加以证明;
的表达式,并用数学归纳法加以证明;(3)求证以
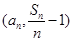 为坐标的点
为坐标的点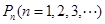 都落在同一直线上。
都落在同一直线上。(1)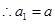
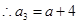 (2)
(2) 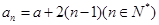
(3)略
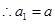
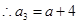 (2)
(2) 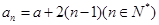
(3)略
本试题主要是考查了数列的通项公式的求解以及数学归纳法证明的综合运用。
解:(1)由已知得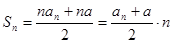
当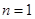 时,
时,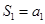 ,
,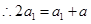 ,
,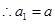
当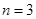 时,
时,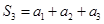 ,
,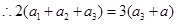
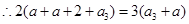 ,
,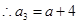 4分
4分
(2)由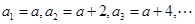 猜想
猜想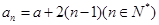
以下数学归纳法证明:
(1)当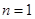 时,左边=
时,左边=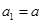 ,右边=
,右边=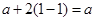 等式成立
等式成立
当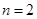 时,左边=
时,左边=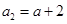 ,右边=
,右边=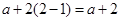 等式成立 6分
等式成立 6分
(2)假设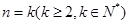 时,等式成立,即
时,等式成立,即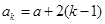
则当 时
时 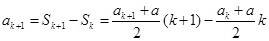
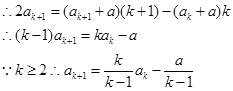
将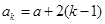 代入,得
代入,得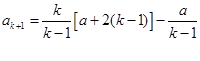
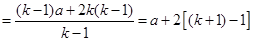
 当
当 时,等式成立
时,等式成立
由(1)、(2)可知,对任意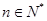 ,等式
,等式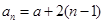 都成立。 10分
都成立。 10分
(3)当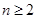 时,
时,
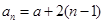 ,
,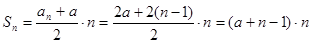
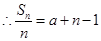
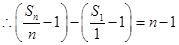 又
又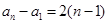
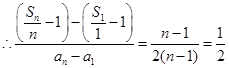
故点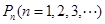 都落在同一直线上.
都落在同一直线上.
解:(1)由已知得
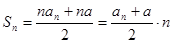
当
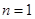 时,
时,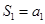 ,
,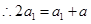 ,
,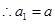
当
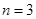 时,
时,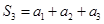 ,
,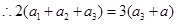
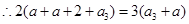 ,
,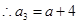 4分
4分(2)由
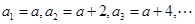 猜想
猜想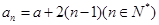
以下数学归纳法证明:
(1)当
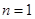 时,左边=
时,左边=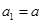 ,右边=
,右边=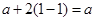 等式成立
等式成立当
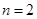 时,左边=
时,左边=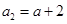 ,右边=
,右边=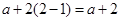 等式成立 6分
等式成立 6分(2)假设
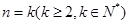 时,等式成立,即
时,等式成立,即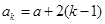
则当
 时
时 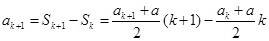
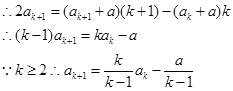
将
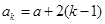 代入,得
代入,得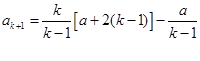
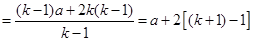
 当
当 时,等式成立
时,等式成立由(1)、(2)可知,对任意
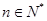 ,等式
,等式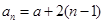 都成立。 10分
都成立。 10分(3)当
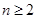 时,
时,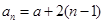 ,
,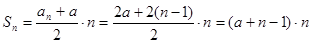
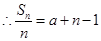
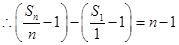 又
又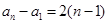
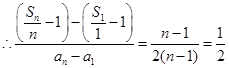
故点
 都落在同一直线上.
都落在同一直线上.
练习册系列答案
相关题目
 中,
中, ,
,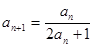 .
.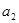 、
、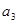 、
、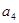 的值;
的值;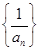 为等差数列.
为等差数列. 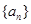 的前n项和为
的前n项和为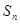 ,且
,且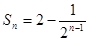 ,数列
,数列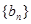 为等差数列,且
为等差数列,且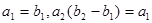 .
. ,求数列
,求数列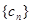 的前n项和
的前n项和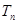 .
.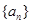 为等差数列,
为等差数列, 为正项等比数列,公比q≠1,若
为正项等比数列,公比q≠1,若 ,则( )
,则( )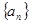 的通项
的通项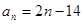 。
。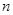 为何值时,前
为何值时,前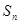 有最小值,并求出这个最小值。
有最小值,并求出这个最小值。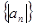 前
前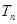 ,求
,求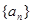 中,已知
中,已知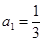 ,
,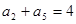 ,
,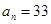 ,则
,则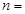 ( )
( )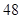
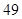
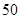

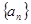 中,有
中,有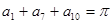 ,则
,则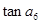 = ▲ 。
= ▲ 。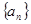 为等差数列,
为等差数列,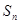 是其前n项的和,且
是其前n项的和,且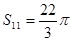 ,则
,则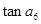 =( )
=( )