已知函数f．的单调性,在x=1处取得极值.不等式f(x)≥bx-2对任意x∈恒成立.求实数b的取值范围．题目和参考答案——青夏教育精英家教网—

题目内容

13．已知函数f（x）=ax-1-lnx（a∈R）．
（Ⅰ）讨论函数f（x）的单调性；
（Ⅱ）若函数f（x）在x=1处取得极值，不等式f（x）≥bx-2对任意x∈（0，+∞）恒成立，求实数b的取值范围．

分析（Ⅰ）对函数进行求导，然后令导函数大于0求出x的范围，令导函数小于0求出x的范围，即可得到答案；
（Ⅱ）由函数f（x）在x=1处取得极值求出a的值，再依据不等式恒成立时所取的条件，求出实数b的取值范围即可．

解答解：（Ⅰ）函数f（x）的定义域为（0，+∞）
.$f'（x）=a-\frac{1}{x}=\frac{ax-1}{x}$．
若a≤0，则f'（x）＜0，
∴f（x）在（0，+∞）上递减；
若a＞0，则由f'（x）＞0得：$x＞\frac{1}{a}$；
由f'（x）＜0得：$0＜x＜\frac{1}{a}$．
∴f（x）在$（0，\frac{1}{a}）$上递减，在$（\frac{1}{a}，+∞）$递增．
（Ⅱ）∵函数f（x）在x=1处取得极值，
∴f'（1）=0，即a-1=0，解得：a=1．
∴f（x）=x-1-lnx．
由f（x）≥bx-2得：x-1-lnx≥bx-2，
∵x＞0，
∴$b≤1+\frac{1}{x}-\frac{lnx}{x}$．
令$g（x）=1+\frac{1}{x}-\frac{lnx}{x}$，
则$g'（x）=\frac{lnx-2}{x^2}$
由g'（x）＞0得：x＞e²；
由g'（x）＜0得：0＜x＜e²．
所以，g（x）在（0，e²）上递减，在（e²，+∞）递增．
∴$g{（x）_{min}}=g（{e^2}）=1-\frac{1}{e^2}$，
∴$b≤1-\frac{1}{e^2}$．

点评本题主要考查导函数的正负与原函数的单调性之间的关系，即当导函数大于0时原函数单调递增，当导函数小于0时原函数单调递减，会利用导数研究函数的单调区间以及根据函数的增减性得到函数的最值．掌握不等式恒成立时所取的条件．

练习册系列答案

4．

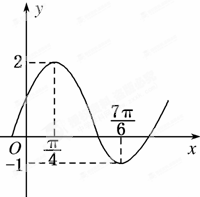将函数f（x）=Asin（ωx+φ）+k（A＞0，ω＞0，0＜φ＜π）的图象向右平移$\frac{2π}{3}$个单位，所得曲线的一部分如图所示，则f（x）的解析式为（　　）

	A．	f（x）=$\frac{3}{2}$sin（$\frac{12}{11}$x-$\frac{21π}{22}$）+1		B．	f（x）=$\frac{3}{2}$sin（$\frac{12}{11}$x+$\frac{21π}{22}$）+$\frac{1}{2}$
	C．	f（x）=2sin（$\frac{11}{12}$x+$\frac{21π}{22}$）-$\frac{1}{2}$		D．	f（x）=$\frac{3}{2}$sin（$\frac{12}{11}$x+$\frac{5π}{22}$）+$\frac{1}{2}$

1．化简或计算下列各式：
（1）16${\;}^{-\frac{1}{2}}}$-（${\frac{1}{2}}$）${\;}^{-\frac{1}{2}}}$-（${\frac{27}{8}}$）${\;}^{\frac{2}{3}}}$+（${\frac{3}{5}}$）⁰+$\root{4}{{{{（1-\sqrt{2}）}^4}}}$；
（2）（a${\;}^{\frac{2}{3}}}$b${\;}^{\frac{1}{2}}}$）×（-3a${\;}^{\frac{1}{2}}}$b${\;}^{\frac{1}{3}}}$）÷（$\frac{1}{3}$a${\;}^{\frac{1}{6}}}$b${\;}^{\frac{5}{6}}}$）．

8．函数f（x）=lgx+$\sqrt{1-x}$的定义域是（　　）

18．已知△ABC的三边长分别为x，4，2x，则其面积的最大值为$\frac{16}{3}$．

5．椭圆x²+4y²=16的长轴长和短轴长依次为（　　）