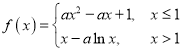题目内容
【题目】某公司新上一条生产线,为保证新的生产线正常工作,需对该生产线进行检测,现从该生产线上随机抽取100件产品,测量产品数据,用统计方法得到样本的平均数![]() ,标准差
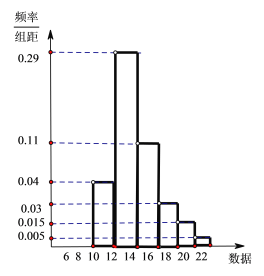
,标准差![]() ,绘制如图所示的频率分布直方图,以频率值作为概率估值。
,绘制如图所示的频率分布直方图,以频率值作为概率估值。
(1)从该生产线加工的产品中任意抽取一件,记其数据为![]() ,依据以下不等式评判(
,依据以下不等式评判(![]() 表示对应事件的概率)
表示对应事件的概率)
①![]()
②![]()
③![]()
评判规则为:若至少满足以上两个不等式,则生产状况为优,无需检修;否则需检修生产线,试判断该生产线是否需要检修;
(2)将数据不在![]() 内的产品视为次品,从该生产线加工的产品中任意抽取2件,次品数记为
内的产品视为次品,从该生产线加工的产品中任意抽取2件,次品数记为![]() ,求
,求![]() 的分布列与数学期望
的分布列与数学期望![]() 。
。
【答案】(1) 不满足至少两个不等式,该生产线需检修;(2)见解析.
【解析】分析:(1)根据频率分布直方图得出X落在![]() 上的概率,从而得出结论;
上的概率,从而得出结论;
(2)根据题意,![]() 的可能值为:0,1,2,分别求出对应的概率即可.
的可能值为:0,1,2,分别求出对应的概率即可.
详解:(1)由题意知![]() ,由频率分布直方图得:
,由频率分布直方图得:
![]()


![]() 不满足至少两个不等式,该生产线需检修。
不满足至少两个不等式,该生产线需检修。
(2)由(1)知:![]()
任取一件是次品的概率为:![]()
任取两件产品得到次品数![]() 的可能值为:0,1,2
的可能值为:0,1,2
则![]()
![]()
![]()
![]()
![]() 的分布列为:
的分布列为:
| 0 | 1 | 2 |
|
|
|
|
![]()
![]()
(或![]() )
)

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
【题目】高三学生为了迎接高考,要经常进行模拟考试,锻炼应试能力,某学生从升入高三到高考要参加![]() 次模拟考试,下面是高三第一学期某学生参加
次模拟考试,下面是高三第一学期某学生参加![]() 次模拟考试的数学成绩表:
次模拟考试的数学成绩表:
模拟考试第 |
|
|
|
|
|
考试成绩 |
|
|
|
|
|
(1)已知该考生的模拟考试成绩![]() 与模拟考试的次数
与模拟考试的次数![]() 满足回归直线方程
满足回归直线方程![]() ,若高考看作第
,若高考看作第![]() 次模拟考试,试估计该考生的高考数学成绩;
次模拟考试,试估计该考生的高考数学成绩;
(2)把![]() 次模拟考试的成绩单放在五个相同的信封中,从中随机抽取
次模拟考试的成绩单放在五个相同的信封中,从中随机抽取![]() 个信封研究成绩,求抽取的
个信封研究成绩,求抽取的![]() 个信封中恰有
个信封中恰有![]() 个成绩不等于平均值
个成绩不等于平均值![]() 的概率.
的概率.
参考公式: ,
,![]() .
.