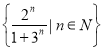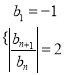题目内容
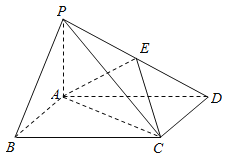
【题目】已知![]() 为定义在实数集
为定义在实数集![]() 上的函数,把方程
上的函数,把方程![]() 称为函数
称为函数![]() 的特征方程,特征方程的两个实根
的特征方程,特征方程的两个实根![]() 、
、![]() (
(![]() ),称为
),称为![]() 的特征根.
的特征根.
(1)讨论函数![]() 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(2)已知![]() 为给定实数,求
为给定实数,求![]() 的表达式;
的表达式;
(3)把函数![]() ,
,![]() 的最大值记作
的最大值记作![]() ,最小值记作
,最小值记作![]() ,研究函数
,研究函数![]() ,
,![]() 的单调性,令
的单调性,令![]() ,若
,若![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)非奇非偶函数;理由见解析
(2)![]()
(3)![]()
【解析】
(1)当![]() 时,判断为奇函数;当
时,判断为奇函数;当![]() 时,取
时,取![]() 和
和![]() ,非奇非偶函数,得到答案.
,非奇非偶函数,得到答案.
(2)根据韦达定理得到![]() ,代入表达式化简得到答案.
,代入表达式化简得到答案.
(3)先证明![]() 在
在![]() 内单调递增,
内单调递增,![]() ,代入不等式得到答案.
,代入不等式得到答案.
(1)当![]() 时,
时,![]() ,
,![]() 是奇函数
是奇函数
当![]() 时,
时,![]() ,
,![]()
![]() 且
且![]() ,
,![]() 是非奇非偶函数
是非奇非偶函数
综上所述:![]() 时,
时,![]() 为奇函数;
为奇函数;![]() 时,
时,![]() 是非奇非偶函数.
是非奇非偶函数.
(2)![]() 恒成立
恒成立
![]()
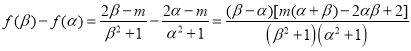

![]() 上是递增函数,设
上是递增函数,设![]()
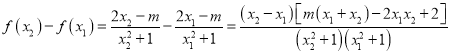
由(2)可知:![]() 、
、![]() 是方程
是方程![]() 的两个实根,
的两个实根,
又![]()
![]()
![]()
![]()
![]()
![]() 在
在![]() 内单调递增,
内单调递增,![]()
![]() 恒成立
恒成立![]()
![]()

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目