题目内容
已知正方形的中心G（-1，0），一条边上所在的直线方程为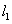
：x+3y-5=0，求正方形其它三边所在直线的方程。
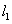：x+3y-5=0，求正方形其它三边所在直线的方程。 解：设与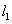
平行的边所在的直线方程是：x+3y+m=0（m≠-5），
与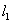
垂直的边坐在的直线方程是：3x-7y+n=0，
设正方形的中心到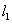
的距离为d，
则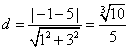
，
所以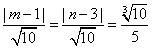
，
解得：m=7或m=-5（舍），n=9或n=-3，
从而，可得其它三边所在的直线方程为：x+3y+7=0，3x-y+9=0，3x-y-3=0。
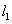平行的边所在的直线方程是：x+3y+m=0（m≠-5），与
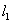垂直的边坐在的直线方程是：3x-7y+n=0，设正方形的中心到
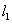的距离为d，则
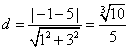，所以
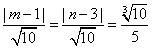，解得：m=7或m=-5（舍），n=9或n=-3，
从而，可得其它三边所在的直线方程为：x+3y+7=0，3x-y+9=0，3x-y-3=0。
练习册系列答案
相关题目
如图是一幅招贴画的示意图，其中ABCD是边长为2a的正方形，周围是四个全等的弓形．已知O为正方形的中心，G为AD的中点，点P在直线OG上，弧AD是以P为圆心、PA为半径的圆的一部分，OG的延长线交弧AD于点H．设弧AD的长为l，
+1，