题目内容
函数f(x)满足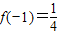 ,对任意x,y∈R有
,对任意x,y∈R有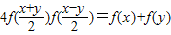 ,则f(-2012) .
,则f(-2012) .
【答案】分析:可采用赋值法求得f(0)= ,再通过赋值法求得f(-2)=f(-4)=f(-6)=-
,再通过赋值法求得f(-2)=f(-4)=f(-6)=- ,从而归纳出结论.
,从而归纳出结论.
解答:解:∵f(-1)= ,令x=y=-1,有4f(-1)f(0)=2f(-1)=
,令x=y=-1,有4f(-1)f(0)=2f(-1)= ,
,
∴f(0)= ,
,
令y=-x,有4f(0)f(x)=f(x)+f(-x),即2f(x)=f(x)+f(-x),
∴f(-x)=f(x),即f(x)为偶函数;
令x=-2,y=0,有4[f(-1)]2=f(-2)+f(0),解得f(-2)=- ①;
①;
令x=-4,y=0,有4[f(-2)]2=f(-4)+f(0),解得f(-4)=- ②;
②;
再令x=4,y=2,有4f(3)f(1)=f(4)+f(2),解得f(3)= ;
;
令x=-6,y=0,有4[f(-3)]2=f(-6)+f(0),解得f(-6)=- ③;
③;
…
∴f(-2n)=- .
.
∴f(-2012)=- .
.
点评:本题考查抽象函数及其用,关键在于通过赋值法寻找规律,难点在于多次赋值才能发现规律,属于难题.
 ,再通过赋值法求得f(-2)=f(-4)=f(-6)=-
,再通过赋值法求得f(-2)=f(-4)=f(-6)=- ,从而归纳出结论.
,从而归纳出结论.解答:解:∵f(-1)=
 ,令x=y=-1,有4f(-1)f(0)=2f(-1)=
,令x=y=-1,有4f(-1)f(0)=2f(-1)= ,
,∴f(0)=
 ,
,令y=-x,有4f(0)f(x)=f(x)+f(-x),即2f(x)=f(x)+f(-x),
∴f(-x)=f(x),即f(x)为偶函数;
令x=-2,y=0,有4[f(-1)]2=f(-2)+f(0),解得f(-2)=-
 ①;
①;令x=-4,y=0,有4[f(-2)]2=f(-4)+f(0),解得f(-4)=-
 ②;
②;再令x=4,y=2,有4f(3)f(1)=f(4)+f(2),解得f(3)=
 ;
;令x=-6,y=0,有4[f(-3)]2=f(-6)+f(0),解得f(-6)=-
 ③;
③;…
∴f(-2n)=-
 .
.∴f(-2012)=-
 .
.点评:本题考查抽象函数及其用,关键在于通过赋值法寻找规律,难点在于多次赋值才能发现规律,属于难题.

练习册系列答案
相关题目
已知函数f(x)满足:对定义域内的任意x,都有f(x+2)+f(x)<2f(x+1),则函数f(x)可以是( )
| A、f(x)=2x+1 | B、f(x)=ex | C、f(x)=lnx | D、f(x)=xsinx |