题目内容
若α,β均为锐角,且cos(
+α)=-
,cos(
-β)=
,则α+β等于( )
| π |
| 2 |
| ||
| 5 |
| π |
| 2 |
| ||
| 10 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:直接利用诱导公式化简已知条件,利用两角和的余弦函数求解即可.
解答:
解:α,β均为锐角,且cos(
+α)=-
,cos(
-β)=
,
所以sinα=
,cosα=
=
,
sinβ=
,coβ=
=
.
cos(α+β)=cosαcosβ-sinαsinβ=
×
-
×
=
.
α,β均为锐角,所以α+β=
.
故选:A.
| π |
| 2 |
| ||
| 5 |
| π |
| 2 |
| ||
| 10 |
所以sinα=
| ||
| 5 |
| 1-sin2α |
2
| ||
| 5 |
sinβ=
| ||
| 10 |
| 1-sin2β |
3
| ||
| 10 |
cos(α+β)=cosαcosβ-sinαsinβ=
2
| ||
| 5 |
3
| ||
| 10 |
| ||
| 5 |
| ||
| 10 |
| ||
| 2 |
α,β均为锐角,所以α+β=
| π |
| 4 |
故选:A.
点评:本题考查诱导公式的应用,同角三角函数的基本关系式以及两角和的余弦函数的应用,考查计算能力.

练习册系列答案
相关题目
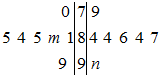 如图是2010年“唱响九江”电视歌手大奖赛中,七位专家评委为甲、乙两名选手打出的分数的茎叶图(其中m,n为数字0~9中的一个),去掉一个最高分和一个最低分后,甲、乙两名选手得分的平均数分别为a1,a2,则一定有( )
如图是2010年“唱响九江”电视歌手大奖赛中,七位专家评委为甲、乙两名选手打出的分数的茎叶图(其中m,n为数字0~9中的一个),去掉一个最高分和一个最低分后,甲、乙两名选手得分的平均数分别为a1,a2,则一定有( )| A、a1>a2 |
| B、a2>a1 |
| C、a1,a2的大小与m的值有关 |
| D、a1,a2的大小与m,n的值都有关 |
下列函数中,在其定义域内既是增函数又是奇函数的是( )
A、y=
| ||
B、y=-
| ||
| C、y=x|x| | ||
| D、y=log2(x-1) |
函数y=
中自变量x的取值范围是( )
| x-2 |
| A、x>2 | B、x<2 |
| C、x≥2 | D、x≤2 |
设集合P={x|x<1},Q={x|x2<4},则P∩Q=( )
| A、{x|-1<x<2} |
| B、{x|-2<x<-1} |
| C、{x|1<x<2} |
| D、{x|-2<x<1} |
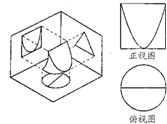 一个圆柱从顶部切掉两块,剩下部分几何体如图所示,此几何体的正视图和俯视图如图所示,其中正视图中的四边形是边长为2的正方形,则此几何体的侧视图的面积为( )
一个圆柱从顶部切掉两块,剩下部分几何体如图所示,此几何体的正视图和俯视图如图所示,其中正视图中的四边形是边长为2的正方形,则此几何体的侧视图的面积为( )