题目内容
设
的内角
所对边的长分别是
，且
，的面积为
，求
与
的值.
，
或
.
解析试题分析：根据三角形面积公式可以求出
，利用
可以解出，对
进行分类讨论，通过余弦定理即可求出
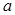的值.
由三角形面积公式，得
，故.
∵，∴
.
当
时，由余弦定理得，
，所以；
当
时，由余弦定理得，
，所以
.
考点：1.三角形面积公式；2.余弦定理.
练习册系列答案
相关题目
题目内容
设的内角所对边的长分别是，且，的面积为，求与的值.
，或.
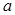解析试题分析：根据三角形面积公式可以求出，利用可以解出，对进行分类讨论，通过余弦定理即可求出的值.
由三角形面积公式，得，故.
∵，∴.
当时，由余弦定理得，，所以；
当时，由余弦定理得，，所以.
考点：1.三角形面积公式；2.余弦定理.
分别为
的三个内角
的对边，且
．
的大小； （2）若
，
为
的中点，求
的长．
。
,求B.
的内角
所对边的长分别是
，且
的值；
的值.
分别为
三个内角
的对边，且
；
,△ABC的面积为
,求
分别为角A、B、C所对的边，已知
，
的值； 
，求△ABC的面积.
中，
，
．
的大小；
，求最小边的边长．