题目内容
已知p:f-1(x)是f(x)=1-3x的反函数，且|f-1(a)|＜2;q:集合A={x|x2+(a+2)x+1=0,x∈R},B={x|x＞0},且A∩B=
.求实数a的取值范围，使p、q中有且只有一个为真命题.
解：∵f(x)=1-3x,?
∴f-1(x)=.?
由|f-1(a)|＜2,得|
|＜2,解得-5＜a＜7.?
当Δ＜0时，A=
，?
此时（a+2）2-4＜0,-4＜a＜0;??
当Δ≥0时，由A∩B=
，得?
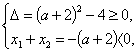解得a≥0.?
由此得a＞-4.?
（1）要使p真q假，则
解得-5＜a≤-4.?
(2)要使p假q真，则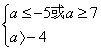
解得a≥7.?
∴当a的取值范围是(-5,-4］∪［7,+∞）时，p、q中有且只有一个为真命题.
练习册系列答案
相关题目
已知函数f（x）=ax（a＞0，a≠1），g（x）=-x2+2x+2，设函数F（x）=min{f（x），g（x）}，（min{p，q}表示p，q中的较小值），若F（x）＜2恒成立，则a的取值范围是（ ）
| A、（1，2） | ||
| B、（0，1）或（1，2） | ||
C、（1，
| ||
D、（0，1）或（1，
|