ћвƒњƒЏ»Ё
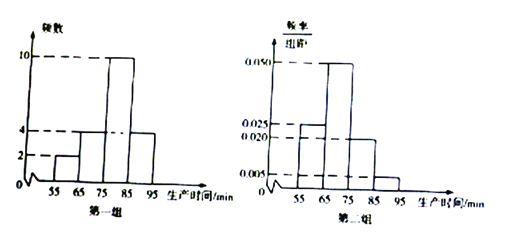
°Њћвƒњ°њƒ≥Єя–£‘Џ2019ƒкµƒ„‘÷ч’–…ъ± ‘≥…Љ®£®¬ъЈ÷200Ј÷£©÷–£ђЋжїъ≥й»°100√ыњЉ…ъµƒ≥…Љ®£ђ∞ііЋ≥…Љ®Ј÷≥…ќе„й£ђµ√µљ»зѕ¬µƒ∆µ¬ Ј÷≤Љ±н£Ї
„йЇ≈ | Ј÷„й | ∆µ э | ∆µ¬ |
µЏ“ї„й |
| 15 |
|
µЏґю„й |
| 25 | 0.25 |
µЏ»э„й |
| 30 | 0.3 |
µЏЋƒ„й |
|
|
|
µЏќе„й |
| 10 | 0.1 |
£®1£©«у∆µ¬ Ј÷≤Љ±н÷–![]() £ђ
£ђ![]() £ђ
£ђ![]() µƒ÷µ£ї
µƒ÷µ£ї
£®2£©єјЉ∆± ‘≥…Љ®µƒ∆љЊщ эЉ∞÷–ќї э£®Ќђ“ї„й÷–µƒ эЊЁ”√Є√„й«шЉдµƒ÷–µг÷µ„чіъ±н£©£ї£®ЊЂ»Јµљ0.1£©
£®3£©»фі”µЏЋƒ„й°ҐµЏќе„йµƒ—І…ъ÷–∞і„й”√Ј÷≤г≥й—щµƒЈљЈ®≥й»°6√ы—І…ъ≤ќЉ”√ж ‘£ђ”√Љтµ•Ћжїъ≥й—щЈљЈ®і”6»Ћ÷–≥й»°2»Ћ„чќ™’э°ҐЄ±–°„й≥§£ђ«у°∞≥й»°µƒ2»Ћќ™Ќђ“ї„й°±µƒЄ≈¬ .
°Њір∞Є°њ£®1£©![]() £ђ
£ђ![]() £ђ
£ђ![]() .£®2£©∆љЊщ э137 ÷–ќї э136.7£®3£©
.£®2£©∆љЊщ э137 ÷–ќї э136.7£®3£©![]()
°Њљвќц°њ
£®1£©∆µ эЇЌќ™100£ђ«у≥ц![]() £ђ”…∆µ э«у≥ц
£ђ”…∆µ э«у≥ц![]() £ї
£ї
£®2£©ЄщЊЁ∆љЊщ эєЂ љ£ђЉіњ…«у≥ц∆љЊщ э£ђЄщЊЁ÷±ЈљЌЉ«у≥ц÷–ќї э£ї
£®3£©ґ‘≥й»°µƒ6√ы—І…ъ±аЇ≈£ђЅ–≥цЋжїъ≥й»°Ѕљ»ЋµƒЋщ”–«йњц£ђ»Јґ®≥ц2»Ћќ™Ќђ“ї„йµƒ≥й»°Єц э£ђ∞і«ує≈µдЄ≈–ЌЄ≈¬ µƒЈљЈ®£ђЉіњ…«уљв.
љв£Ї£®1£©“јћв“в£Ї![]() £ђ
£ђ![]() £ђ
£ђ![]() .
.
£®2£©± ‘≥…Љ®µƒ∆љЊщ эќ™£Ї
![]()
![]() .
.
“тќ™µЏ1„й”лµЏ2„йµƒ∆µ¬ ÷ЃЇЌќ™£Ї0.4£ђ
Ћщ“‘÷–ќї эќ™£Ї![]() .
.
£®3£©“јћв“в£ЇµЏ4„й≥й»°4»Ћ£ђЉ«ќ™£Ї![]() £ђ
£ђ![]() £ђ
£ђ![]() £ђ
£ђ![]() £ђ
£ђ
µЏ5„й≥й»°2»Ћ£ђЉ«ќ™£Ї![]() £ђ
£ђ![]() £ђ
£ђ
‘тїщ±Њ ¬Љюќ™£Ї![]() £ђ
£ђ![]() £ђ
£ђ![]() £ђ
£ђ![]() £ђ
£ђ![]() £ђ
£ђ
![]() £ђ
£ђ![]() £ђ
£ђ![]() £ђ
£ђ![]() £ђ
£ђ![]() £ђ
£ђ![]() £ђ
£ђ![]() £ђ
£ђ
![]() £ђ
£ђ![]() £ђ
£ђ![]() є≤15÷÷£ђ∆д÷–¬ъ„гћв“вµƒ”–7÷÷.
є≤15÷÷£ђ∆д÷–¬ъ„гћв“вµƒ”–7÷÷.
Ћщ“‘Ћщ«уЄ≈¬ ќ™£Ї![]() .
.

 √ы–£њќћ√ѕµЅ–ір∞Є
√ы–£њќћ√ѕµЅ–ір∞Є