题目内容
【题目】（5分）《九章算术》“竹九节”问题：现有一根9节的竹子，自上而下各节的容积成等差数列，上面4节的容积共3升，下面3节的容积共4升，则第五节的容积为（ ）
A. 1升 B. 
升 C. 
升 D. 
升
【答案】B
【解析】试题设出竹子自上而下各节的容积且为等差数列，根据上面4节的容积共3升，下面3节的容积共4升列出关于首项和公差的方程，联立即可求出首项和公差，根据求出的首项和公差，利用等差数列的通项公式即可求出第5节的容积．
解：设竹子自上而下各节的容积分别为：a1，a2，…，a9，且为等差数列，
根据题意得：a1+a2+a3+a4=3，a7+a8+a9=4，
即4a1+6d=3①，3a1+21d=4②，②×4﹣①×3得：66d=7，解得d=
，
把d=代入①得：a1=
，
则a5=+（5﹣1）=
．
故选B
挑战100单元检测试卷系列答案
【题目】某单位员工
人参加“学雷锋”志愿活动，按年龄分组：第
组
，第
组
,第
组
,第
组
,第
组
，得到的频率分布直方图如图所示.
（1）下表是年龄的频率分布表，求正整数
的值；
区间 |
|
|
|
|
|
人数 |
|
|
|
|
|
（2）现在要从年龄较小的第
组中用分层抽样的方法抽取
人，年龄在第组抽取的员工的人数分别是多少？
（3）在（2）的前提下，从这人中随机抽取人参加社区宣传交流活动，求至少有人年龄在第组的概率.
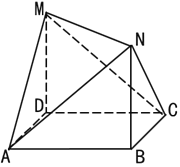
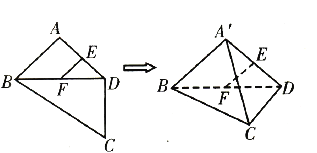
【题目】如图，平面四边形
中，
，
是
，
中点，
，
，
，将
沿对角线折起至
，使平面
平面
，则四面体
中，下列结论不正确的是（ ）
A. 
平面
B. 异面直线
与
所成的角为
C. 异面直线
与
所成的角为
D. 直线与平面所成的角为
【题目】某高校在2019年的自主招生笔试成绩（满分200分）中，随机抽取100名考生的成绩，按此成绩分成五组，得到如下的频率分布表：
组号 | 分组 | 频数 | 频率 |
第一组 |
| 15 |
|
第二组 |
| 25 | 0.25 |
第三组 |
| 30 | 0.3 |
第四组 |
|
|
|
第五组 |
| 10 | 0.1 |
（1）求频率分布表中
，
，
的值；
（2）估计笔试成绩的平均数及中位数（同一组中的数据用该组区间的中点值作代表）；（精确到0.1）
（3）若从第四组、第五组的学生中按组用分层抽样的方法抽取6名学生参加面试，用简单随机抽样方法从6人中抽取2人作为正、副小组长，求“抽取的2人为同一组”的概率.