题目内容
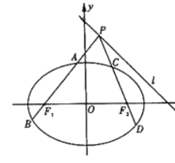
【题目】在平面直角坐标系xOy中,过点P(0,1)且互相垂直的两条直线分別与圆O:![]() 交于点A,B,与圆M:(x﹣2)2+(y﹣1)2=1交于点C,D.
交于点A,B,与圆M:(x﹣2)2+(y﹣1)2=1交于点C,D.
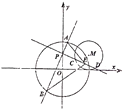
(1)若AB=![]() ,求CD的长;
,求CD的长;
(2)若CD中点为E,求△ABE面积的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)先由AB的长度求出圆心O到直线AB的距离,列方程求出直线AB的斜率,从而得到直线CD的斜率,写出直线CD的方程,用垂径定理求CD得长度;(2)△ABE的面积![]() ,先考虑直线AB、CD平行于坐标轴的情况,不平行时先由垂径定理求出AB,再在△PME 中用勾股定理求出PE,将面积S表示成直线AB斜率k的函数式,再求其范围.
,先考虑直线AB、CD平行于坐标轴的情况,不平行时先由垂径定理求出AB,再在△PME 中用勾股定理求出PE,将面积S表示成直线AB斜率k的函数式,再求其范围.
解:(1)因为AB=![]() ,圆O半径为2
,圆O半径为2
所以点O到直线AB的距离为![]()
显然AB、CD都不平行于坐标轴
可设AB:![]() ,即
,即![]()
则点O到直线AB的距离![]() ,解得
,解得![]()
因为AB⊥CD,所以![]()
所以CD:![]() ,即
,即![]()
点M(2,1)到直线CD的距离![]()
所以![]()
(2)当AB⊥x轴,CD∥x轴时,此时AB=4,点E与点M重合,PM=2,所以△ABE的面积S=4
当AB∥x轴,CD⊥x轴时,显然不存在,舍
当AB与CD都不平行于坐标轴时
由(1)知![]()
因为![]() ,所以
,所以![]()
因为点E是CD中点,所以ME⊥CD,
所以![]()
所以△ABE的面积![]()
记![]() ,则
,则![]()
则![]()
综上所述:![]()

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
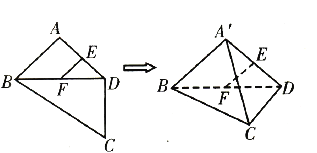
小学生10分钟应用题系列答案【题目】如图,平面四边形![]() 中,
中,![]() ,
,![]() 是
是![]() ,
,![]() 中点,
中点,![]() ,
,![]() ,
,![]() ,将
,将![]() 沿对角线
沿对角线![]() 折起至
折起至![]() ,使平面
,使平面![]() 平面
平面![]() ,则四面体
,则四面体![]() 中,下列结论不正确的是( )
中,下列结论不正确的是( )
A. ![]() 平面
平面![]()
B. 异面直线![]() 与
与![]() 所成的角为
所成的角为![]()
C. 异面直线![]() 与
与![]() 所成的角为
所成的角为![]()
D. 直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]()
【题目】某地区高考实行新方案,规定:语文、数学和英语是考生的必考科目,考生还须从物理、化学、生物、历史、地理和政治六个科目中选出了三个科目作为选考科目.若一名学生从六个科目中选出了三个科目作为选考科目,则称该学生的选考方案确定;否则,称该学生选考方案待确定.某学校为了了解高一年级200名学生选考科目的意向,随机选取20名学生进行了一次调查,统计选考科目人数如下表:
性别 | 选考方案确定情况 | 物理 | 化学 | 生物 | 历史 | 地理 | 政治 |
男生 | 选考方案确定的有5人 | 5 | 5 | 2 | 1 | 2 | 0 |
选考方案待确定的有7人 | 6 | 4 | 3 | 2 | 4 | 2 | |
女生 | 选考方案确定的有6人 | 3 | 5 | 2 | 3 | 3 | 2 |
选考方案待确定的有2人 | 1 | 2 | 1 | 0 | 1 | 1 |
(1)在选考方案确定的男生中,同时选考物理、化学、生物的人数有多少?
(2)从选考方案确定的男生中任选2名,试求出这2名学生选考科目完全相同的概率.
【题目】某高校在2019年的自主招生笔试成绩(满分200分)中,随机抽取100名考生的成绩,按此成绩分成五组,得到如下的频率分布表:
组号 | 分组 | 频数 | 频率 |
第一组 |
| 15 |
|
第二组 |
| 25 | 0.25 |
第三组 |
| 30 | 0.3 |
第四组 |
|
|
|
第五组 |
| 10 | 0.1 |
(1)求频率分布表中![]() ,
,![]() ,
,![]() 的值;
的值;
(2)估计笔试成绩的平均数及中位数(同一组中的数据用该组区间的中点值作代表);(精确到0.1)
(3)若从第四组、第五组的学生中按组用分层抽样的方法抽取6名学生参加面试,用简单随机抽样方法从6人中抽取2人作为正、副小组长,求“抽取的2人为同一组”的概率.