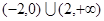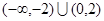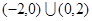题目内容
设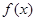 是定义在R上的周期函数,周期为
是定义在R上的周期函数,周期为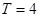 ,对
,对 都有
都有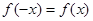 ,且当
,且当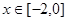 时,
时,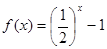 ,若在区间
,若在区间 内关于x的方程
内关于x的方程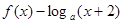 =0
=0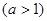 恰有3个不同的实根,则a的取值范围是( )
恰有3个不同的实根,则a的取值范围是( )
| A.(1,2) | B.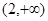 | C.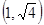 | D.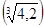 |
D
解析试题分析: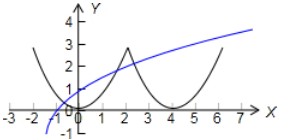
因为对于任意的 ,都有
,都有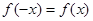 ,所以
,所以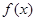 是偶函数,关于
是偶函数,关于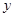 轴对称,又周期
轴对称,又周期
为4,所以函数关于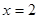 也对称,又当
也对称,又当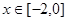 时,
时,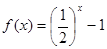 ,若在区间
,若在区间
内关于x的方程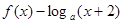 =0恰有3个不同的实根,则函数
=0恰有3个不同的实根,则函数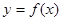 与
与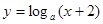 在区间
在区间 上有三个不同的交点,如图所示:
上有三个不同的交点,如图所示:
又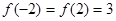 ,则有
,则有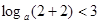 ,且
,且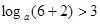 ,解得
,解得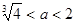 .
.
考点:函数零点与方程根的关系
点评:将方程的根的问题转化成函数零点问题,是解决本题的关键,体现了转化和数形结合
的数学思想,属中档题.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
函数 是【 】.
是【 】.
A.最小正周期为 的奇函数 的奇函数 | B.最小正周期为 的奇函数 的奇函数 |
C.最小正周期为 的偶函数 的偶函数 | D.最小正周期为 的偶函数 的偶函数 |
已知函数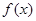 对定义域
对定义域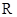 内的任意
内的任意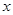 都有
都有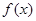 =
=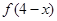 ,且当
,且当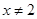 时其导函数
时其导函数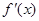 满足
满足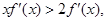 若
若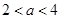 则
则
A.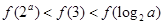 | B.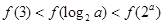 |
C.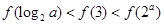 | D.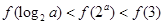 |
下列函数中x=0是极值点的函数是( )
A.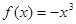 | B.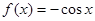 | C.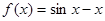 | D.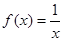 |
设函数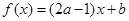 是
是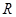 上的减函数,则有( )
上的减函数,则有( )
A.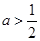 | B.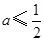 | C.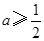 | D.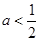 |
 是定义在
是定义在 上的非负可导函数,且满足
上的非负可导函数,且满足 ,对任意正数
,对任意正数 ,若
,若 ,则必有( )
,则必有( )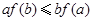



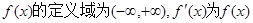 的导函数,函数
的导函数,函数 的图象如右图所示,且
的图象如右图所示,且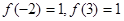 ,则不等式
,则不等式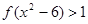 的解集为( )
的解集为( )
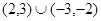

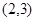
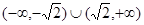
 在定义域内可导,
在定义域内可导, 的图象如图所示,则导函数
的图象如图所示,则导函数 可能为( )
可能为( )

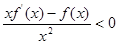 成立,则不等式
成立,则不等式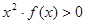 的解集是( )
的解集是( )