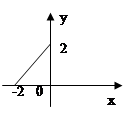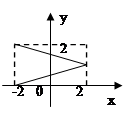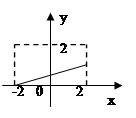题目内容
 在定义域内可导,
在定义域内可导, 的图象如图所示,则导函数
的图象如图所示,则导函数 可能为( )
可能为( )

D
解析试题分析:当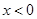 时,原函数是增函数,所以
时,原函数是增函数,所以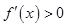 ,当
,当 时原函数先增后减再增,所以导数值先正后负再正,综上D符合要求
时原函数先增后减再增,所以导数值先正后负再正,综上D符合要求
考点:函数单调性与导数关系
点评:函数单调性与其导数的关系:若在某一区间上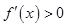 ,则函数
,则函数 是增函数;若
是增函数;若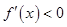 ,则函数
,则函数 是减函数
是减函数

练习册系列答案
相关题目
设函数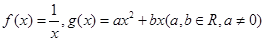 ,若
,若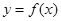 的图象与
的图象与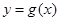 图象有且仅有两个不同的公共点
图象有且仅有两个不同的公共点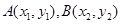 ,则下列判断正确的是( )
,则下列判断正确的是( )
A.当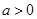 时, 时,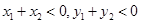 |
B.当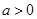 时, 时,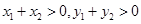 |
C.当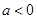 时, 时,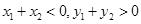 |
D.当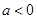 时, 时,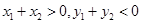 |
设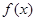 是定义在R上的周期函数,周期为
是定义在R上的周期函数,周期为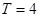 ,对
,对 都有
都有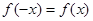 ,且当
,且当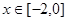 时,
时,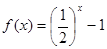 ,若在区间
,若在区间 内关于x的方程
内关于x的方程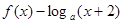 =0
=0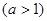 恰有3个不同的实根,则a的取值范围是( )
恰有3个不同的实根,则a的取值范围是( )
| A.(1,2) | B.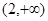 | C.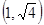 | D.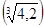 |
已知函数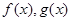 是定义在R上可导函数,满足
是定义在R上可导函数,满足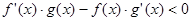 ,且
,且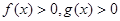 ,对
,对 时。下列式子正确的是( )
时。下列式子正确的是( )
A. | B.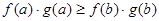 |
C.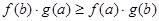 | D.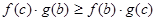 |
函数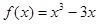 的递减区间是
的递减区间是
A. 或 或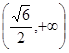 | B.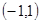 |
C.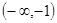 或 或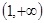 | D.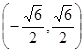 |
给右图的容器甲注水,下面图像中哪一个图像可以大致刻画容器中水的高度与时间的函数关系:( )。
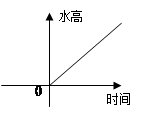
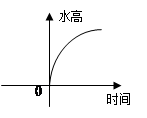
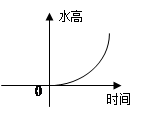

| A. | B. | C. | D. |
函数y=xlnx在区间 (0,1)上是 ( )
| A.单调增函数 |
| B.单调减函数 |
C.在(0,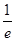 )上是减函数,在( )上是减函数,在(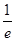 ,1)上是增函数 ,1)上是增函数 |
D.在(0,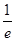 )上是增函数,在( )上是增函数,在(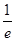 ,1)上是减函数 ,1)上是减函数 |
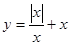 的图象是( )
的图象是( )
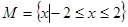 ,
, ,给出下列四个图形,其中能表示以M为定义域,N为值域的函数关系的是( )。
,给出下列四个图形,其中能表示以M为定义域,N为值域的函数关系的是( )。