题目内容
已知sinα= ,sinβ=
,sinβ= 且α、β为锐角,则α+β为
且α、β为锐角,则α+β为
- A.

- B.
 或
或
- C.

- D.非以上答案
A
分析:利用sin2α+cos2α=1可求得cosα,同理可求得cosβ,再由两角和与差的余弦函数即可求得α+β的余弦,从而可求得α+β.
解答:∵sinα= ,sinβ=
,sinβ= 且α、β为锐角,
且α、β为锐角,
∴cosα= ,cosβ=
,cosβ= ,
,
∴cos(α+β)=cosαcosβ-sinαsinβ= ×
× -
- ×
× =
= ,
,
∵α、β为锐角,
∴0<α+β<π,
∴α+β= .
.
故选A.
点评:本题考查sin2α+cos2α=1的应用,考查两角和与差的余弦,考查运算能力,属于中档题.
分析:利用sin2α+cos2α=1可求得cosα,同理可求得cosβ,再由两角和与差的余弦函数即可求得α+β的余弦,从而可求得α+β.
解答:∵sinα=
 ,sinβ=
,sinβ= 且α、β为锐角,
且α、β为锐角,∴cosα=
 ,cosβ=
,cosβ= ,
,∴cos(α+β)=cosαcosβ-sinαsinβ=
 ×
× -
- ×
× =
= ,
,∵α、β为锐角,
∴0<α+β<π,
∴α+β=
 .
.故选A.
点评:本题考查sin2α+cos2α=1的应用,考查两角和与差的余弦,考查运算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
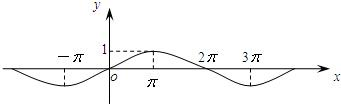 已知函数y=sinωx(ω>0)的图象如图所示,把y=sinωx的图象向右平移
已知函数y=sinωx(ω>0)的图象如图所示,把y=sinωx的图象向右平移| 2π |
| 3 |
A、sin(2x-
| ||||
B、sin(2x-
| ||||
C、sin(
| ||||
D、sin(
|
已知
=-
,则cosα+sinα等于( )
| cos(π-2α) | ||
sin(α-
|
| ||
| 2 |
A、-
| ||||
B、
| ||||
C、
| ||||
D、-
|