题目内容
(08年五市联考理) (13分)椭圆![]() :
:![]() 的两焦点为
的两焦点为![]() ,椭圆上存在点
,椭圆上存在点![]() 使
使![]()
(1)求椭圆离心率![]() 的取值范围;
的取值范围;
(2)当离心率![]() 取最小值时,点
取最小值时,点![]() 到椭圆上的点的最远距离为
到椭圆上的点的最远距离为![]()
①求此时椭圆![]() 的方程;
的方程;
②设斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,
,![]() 为
为![]() 的中点,问
的中点,问![]() 两点能否关于过
两点能否关于过![]() 、
、![]() 的直线对称?若能,求出
的直线对称?若能,求出![]() 的取值范围;若不能,请说明理由。
的取值范围;若不能,请说明理由。
解析:(1)设![]() ……①
……①
将![]() 代入①得
代入①得![]()
![]() 求得
求得![]() ……4分
……4分
(2)①![]() 时,设椭圆方程为
时,设椭圆方程为![]() ,
,![]() 是椭圆上任一点,
是椭圆上任一点,
则![]()
()若![]() ,则
,则![]() 时,
时,![]()
∴![]() ,此时椭圆方程为
,此时椭圆方程为![]() …………………7分
…………………7分
()若![]() ,则
,则![]() 时,
时,![]() ∴
∴![]() ,矛盾
,矛盾
综合得椭圆方程为![]() …………………………………9分
…………………………………9分
②由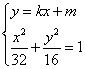 得
得![]()
可求得![]() ,由
,由![]() 求得
求得![]() ,
,
代入![]() 解得
解得![]() ………………13分
………………13分

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
