题目内容
(2012•广东)对任意两个非零的平面向量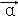 和
和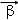 ,定义
,定义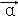 ○
○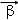 =
=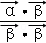 ,若平面向量
,若平面向量 、
、 满足|
满足| |≥|
|≥| |>0,
|>0, 与
与 的夹角
的夹角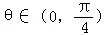 ,且
,且 ○
○ 和
和 ○
○ 都在集合
都在集合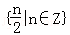 中,则
中,则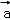 ○
○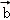 =( )
=( )
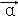 和
和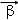 ,定义
,定义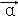 ○
○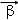 =
=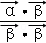 ,若平面向量
,若平面向量 、
、 满足|
满足| |≥|
|≥| |>0,
|>0, 与
与 的夹角
的夹角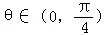 ,且
,且 ○
○ 和
和 ○
○ 都在集合
都在集合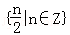 中,则
中,则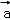 ○
○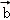 =( )
=( )A.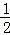 | B.1 | C.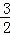 | D.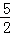 |
C
由题意可得  •
• =
= =
= =
= =
= .
.
同理可得 •
• =
= =
= =
= =
= .
.
由于| |≥|
|≥| |>0,∴n≥m 且 m、n∈z.
|>0,∴n≥m 且 m、n∈z.
∴cos2θ= .再由
.再由 与
与 的夹角θ∈(0,
的夹角θ∈(0, ),可得 cos2θ∈(
),可得 cos2θ∈( ,1),即
,1),即 ∈(
∈( ,1).
,1).
故有 n=3,m=1,∴ •
• =
= =
= ,
,
故选C.
 •
• =
= =
= =
= =
= .
.同理可得
 •
• =
= =
= =
= =
= .
.由于|
 |≥|
|≥| |>0,∴n≥m 且 m、n∈z.
|>0,∴n≥m 且 m、n∈z.∴cos2θ=
 .再由
.再由 与
与 的夹角θ∈(0,
的夹角θ∈(0, ),可得 cos2θ∈(
),可得 cos2θ∈( ,1),即
,1),即 ∈(
∈( ,1).
,1).故有 n=3,m=1,∴
 •
• =
= =
= ,
,故选C.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
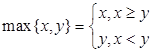 ,
, ,设
,设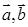 为平面向量,则( )
为平面向量,则( )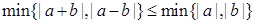
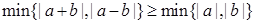
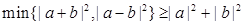
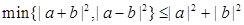
 的边长为
的边长为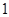 ,
,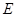 在
在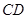 延长线上,且
延长线上,且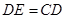 .动点
.动点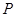 从点
从点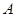 出发,沿正方形
出发,沿正方形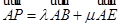 ,则下列命题正确的是 .(填上所有正确命题的序号)
,则下列命题正确的是 .(填上所有正确命题的序号)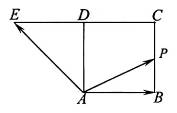
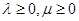 ;
;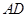 中点时,
中点时,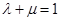 ;
;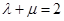 ,则点
,则点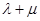 的最大值为
的最大值为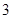 ;
;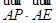 的最大值为
的最大值为 个非零向量
个非零向量 ,且
,且 ,各向量的横坐标和纵坐标均为非负实数,若
,各向量的横坐标和纵坐标均为非负实数,若 (常数),则
(常数),则 的最小值为 .
的最小值为 .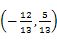 ,θ为a与b的夹角.
,θ为a与b的夹角.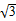 sin2(θ-x),求f(x)的单调递增区间.
sin2(θ-x),求f(x)的单调递增区间. 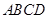 中,
中,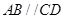 ,
,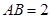 ,
,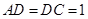 ,
,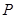 是线段
是线段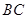 上一动点,
上一动点,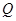 是线段
是线段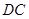 上一动点,
上一动点,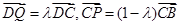 ,则
,则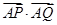 的取值范围是 .
的取值范围是 .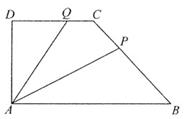
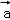 =(3,0),
=(3,0),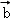 =(0,1),若
=(0,1),若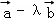 与
与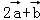 共线,则实数的λ值为( )
共线,则实数的λ值为( )
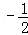
 的河流中,有一艘船正沿与水流垂直的方向以
的河流中,有一艘船正沿与水流垂直的方向以 的速度航行,则船自身航行速度大小为____________
的速度航行,则船自身航行速度大小为____________ .
. ,若
,若 的夹角为
的夹角为 ,则
,则 = .
= .