题目内容
【题目】已知可导函数f（x）的定义域为
，且满足
，
，则对任意的
，“
”是“
”的( )
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
【答案】C
【解析】
由题可得函数f（x）关于直线x=2对称，且在
单调递减，在
单调递增，从充分性，必要性两方面分别说明得出对任意的
，“
”是“
”的充要条件.
f（x）满足f（x+4）=f（﹣x），∴函数f（x）关于直线x=2对称，则
，
∵
，∴
时，
，函数f（x）单调递减；
时，
，函数f（x）单调递增.
先看充分性：
若
，符合，得；
若
，
得
即，
若
，则
，不符合，
故对任意的，“”是“”的充分条件；
再看必要性：
若且，得
，
若
，则得，有，
若
，则
，则有
，
故对任意的，“”是“”的必要条件；
综上，对任意的，“”是“”的充要条件
故选：C
练习册系列答案
相关题目
【题目】某科研小组为了研究一种治疗新冠肺炎患者的新药的效果，选50名患者服药一段时间后，记录了这些患者的生理指标
和
的数据，并统计得到如下的
列联表（不完整）：
|
| 合计 | |
| 12 | 36 | |
| 7 | ||
合计 |
其中在生理指标
的人中，设
组为生理指标
的人，
组为生理指标
的人，他们服用这种药物后的康复时间（单位：天）记录如下：
组：10，11，12，13，14，15，16
组：12，13，15，16，17，14，25
（Ⅰ）填写上表，并判断是否有95%的把握认为患者的两项生理指标
和有关系；
（Ⅱ）从，两组随机各选1人，组选出的人记为甲，组选出的人记为乙，求甲的康复时间比乙的康复时间长的概率．
附：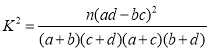
，其中
．
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
